树

二叉树

三种遍历

前中后序遍历的区别其实就是根节点的位置不同：

前序遍历是 根–左子–右子

中序遍历是 左子–根–右子

后序遍历是 左子–右子–根

前序遍历（Preorder Traversal）

• 顺序：根节点 → 左子树 → 右子树
• 特点：先访问根节点，再递归遍历左右子树。
• 示例：

    1
   / \
  2   3
 / \
4   5

前序遍历结果：1, 2, 4, 5, 3

中序遍历（Inorder Traversal）

• 顺序：左子树 → 根节点 → 右子树
• 特点：先遍历左子树，再访问根节点，最后遍历右子树。
• 示例：
  同一棵树的遍历结果：4, 2, 5, 1, 3

后序遍历（Postorder Traversal）

• 顺序：左子树 → 右子树 → 根节点
• 特点：先递归遍历左右子树，最后访问根节点。
• 示例：
  同一棵树的遍历结果：4, 5, 2, 3, 1

完全二叉树

完全二叉树的性质：

对于任意一个节点$i$，其父亲节点是$\dfrac{i}{2}$，左子节点是$2 \times i$，右子节点是$2 \times i+1$。

树状数组

可以高效率地查询和维护前缀和(或区间和)；当序列是动态变化的时，如果改变其中一个元素$a_i$的值，那么后面的前缀和都要重新计算，查询一次的复杂度就会变成$O(n)$。但是树状数组可以用简短的代码大大提高效率，查询和维护的复杂度都为$O(log_2n)$。

lowbit(x)

找x的二进制数的最后一个1对应的十进制是多少，找到的数一定是2的次幂。

lowbit(x) = x & -x

例如，lowbit(5) = 5 & -5 = 1，

lowbit(6) = 6 & -6 = 2，lowbit(8) = 8 & -8 = 8

编码

#incldue <bits/stdc++.h>
using namespace std;
const int N = 1000;
#define lowbit(x) ((x) & -(x))
int tree[N] = {0};

void update(int x,int d){    //单点修改:修改元素a[x], a[x] = a[x] + d;
    while(x <= N){
        tree[x] += d;
        x += lowbit(x);
    }
}

int sum(int x){        //查询前缀和:返回前缀和sum[x] = a[1] + a[2] +...+ a[x]
    int ans = 0;
    while(x > 0){
        ans += tree[x];
        x -= lowbit(x);
    }
    return ans;
}
//以上是树状数组相关
int a[11] = {0,4,5,6,7,8,9,10,11,12,13}        //注意a[0]拿来占位的，不用

int main(){
    for(int i=1;i<=10;i++)
        update(i,a[i]);        //初始化tree[]数组
    cout << "old:[5,8] = "<< sum(8) - sum(4) << '\n'; //查询区间和[5,8] = 38
    update(5,100);        //修改a[5]增加100
    cout << "new:[5,8] = "<< sum(8) - sum(4) << '\n'; //查询新和 = 138
    return 0;
}

线段树

线段树的核心思想是分治，大区间的解可以由小区间的解合并而来，总复杂度为$O(nlogn)$。有两个基本应用场景：

1. 区间最值问题。长为$n$的序列$a$，需要以下操作：
   1. 求区间$[i,j]$内的最值
   2. 修改$a[k]$为$x$
2. 区间和问题。长为$n$的序列$a$，先更改某些数的值，再求区间$[ i , j ]$的和。

线段树建立在二叉树上，每次分治左右子树各一半，能利用二叉树的许多性质。

PS：对于任意一个节点$i$其父亲节点是$\dfrac{i}{2}$，其左孩子是$2 \times i$，其右孩子是$2 \times i+1$。

考察每个线段$[L,R]$，$L$是左端，$R$是右端：

1. $L=R$，说明这个节点只有一个元素，它是叶子节点。
2. $L<R$，说明这个节点代表的不止一个点，那么它有两个孩子，左孩子区间为$[L,M]$，右孩子区间为$[M+1,R]$，其中$M = (L+R)/2$。

线段树的构造：

//定义根节点是tree[1]，即编号为1的节点是根
int tree[N*4];            //用tree[i]记录线段i的最值或区间和
//p是父节点，ls(p)是左儿子，rs(p)是右儿子
int ls(int p){return p<<1;}        //左儿子，编号是p*2
int rs(int p){return p<<1|1;}    //右儿子，编号是p*2+1

void push_up(int p){                        //从下向上传递区间值
    tree[p] = tree[ls(p)] + tree[rs(p)];    //区间和
  //tree[p] = min(tree[ls(p)],tree[rs(p)]); //最小值
}

void build(int p,int pl,int pr){            //节点编号p指向区间[pl,pr]
    if(pl == pr) {tree[p] = a[pl];return;}  //最底层的叶子节点，存叶子节点的值
    int mid = (pl+pr) >> 1;                    //分治：折半
    build(ls(p),pl,mid);                    //递归左儿子
    build(rs(p),mid+1,pr);                    //递归右儿子
    push_up(p);                                //从下往上传递区间值
}

区间查询：

int query(int L,int R,int p,int pl,int pr){
    if(L<=pl && R>=pr) return tree[p];                //完全覆盖
    int mid = (pl+pr) >> 1;
    if(L<=mid)      res += query(L,R,ls(p),pl,mid);	//L与左子节点有重叠
    if(R>=mid+1) res += queru(L,R,rs(p),mid+1,pr);    //R与右子节点有重叠
    return res;
}    //调用方式 query(L,R,1,1,n);

Layz-Tag:

线段树的节点$tree[i]$记录区间$i$的值，那么可以再定义一个$tag[i]$，用它统一记录区间$i$的修改。每次修改的复杂度为$O(log_2n)$，一共$m$次操作，总复杂度$O(mlog_2n)$。

区间修改update()

先找到具体区间，对该节点即以上的节点做修改，并给该节点打tag。下次经过某节点且该节点tag不为0，那么就要把tag[p]传递给左右子树，并清空tag[p]，这个过程用push_down()函数完成。

模板(洛谷 P3372)

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+10;
ll a[N];    //记录题目给出的数列的元素,从a[1]开始 
ll tree[N<<2];    //tree[i]为第i个节点的值，表示一个线段的值，如最值，区间和
ll tag[N<<2];    //tag[i]为第i个节点的Lazy-Tag,统一记录这个区间的修改
ll ls(ll p){return p<<1;}    //定位左儿子: p*2
ll rs(ll p){return p<<1|1;}    //定位右儿子: p*2+1
void push_up(ll p){        //从下向上传递区间值 
    tree[p] = tree[ls(p)] + tree[rs(p)]; //求区间和 
  //tree[p] = min(tree[ls(p)],tree[rs(p)]); 求最小值 
}
void build(ll p,ll pl, ll pr){//建树。p为节点编号，指向区间[pl,pr] 
    tag[p] = 0;  //Lazy-Tag标记 
    if(pl == pr){tree[p] = a[pl];return;}  //最底层的叶子，赋值 
    ll mid = (pl + pr) >> 1;  //分治，折半
    build(ls(p),pl,mid);	  //左儿子 
    build(rs(p),mid+1,pr);	  //右儿子
    push_up(p);				  //从下往上传递区间值 
}
void addtag(ll p,ll pl,ll pr,ll d){ //给节点ptag标记，并更新tree 
    tag[p] += d;			//打上tag标记 
    tree[p] += d*(pr-pl+1); //计算新的tree 
}
void push_down(ll p,ll pl,ll pr){  //不能覆盖时，把tag传给子树 
    if(tag[p]){		//有tag标记，以前修改留下的 
        ll mid = (pl+pr)>>1;
        addtag(ls(p),pl,mid,tag[p]);	//tag传给左子树 
        addtag(rs(p),mid+1,pr,tag[p]);	//tag传给右子树 
        tag[p] = 0;		//自己的tag清零 
    }
}
void update(ll L,ll R,ll p, ll pl,ll pr,ll d){ //区间修改，每个元素加d 
    if(L<=pl && pr<=R){		//完全覆盖，直接返回这个节点，它的子树不用继续再深入
        addtag(p,pl,pr,d);  //给p节点打标记，下一次修改会用到 
        return;
    }
    push_down(p,pl,pr);	 //如果不能覆盖，就把tag传给子树
    ll mid = (pl+pr)>>1;
    if(L <= mid) update(L,R,ls(p),pl,mid,d);	//递归左子树
    if(R > mid) update(L,R,rs(p),mid+1,pr,d);	//递归右子树
    push_up(p);	//更新 
}
ll query(ll L,ll R,ll p,ll pl,ll pr){
    //查询区间[L,R],P是当前节点(线段)的编号，[pl,pr]是节点p表示的线段区间
    if(pl >= L&&R >= pr) return tree[p];	//完全覆盖，直接返回
    push_down(p,pl,pr);		//不能覆盖，递归子树
    ll res = 0;
    ll mid = (pl+pr)>>1;
    if(L<=mid) res+=query(L,R,ls(p),pl,mid);  //左子节点有重叠
    if(R>mid) res+=query(L,R,rs(p),mid+1,pr); //右子节点有重叠
    return res; 
}
int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    ll n,m;
    cin >> n >> m;
    for(ll i=1;i<=n;i++)
        cin >> a[i];
    build(1,1,n);		//建树 
    while(m--){
        ll q,L,R,d;
        cin >> q;
        if(q == 1){		//区间修改，每个元素加d 
            cin >> L >> R >> d;
            update(L,R,1,1,n,d);
        }
        else{			//区间查询，[L,R]区间和 
            cin >> L >> R;
            cout << query(L,R,1,1,n) << '\n';
        }
    }
    return 0;
}

以下是线段树模板类模板，目前是求区间和，以后会更新求区间最大值，最小值等等功能

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ull = unsigned long long;
using pii = pair<int,int>;
using pll = pair<ll,ll>;
using pull = pair<ull,ull>;
using vec = vector<int>;
using vecl = vector<ll>; 
using maii = map<int,int>;
#define pb(x) push_back(x) 
const int maxn = 2e5+5;

int a[2*maxn];

template<class T>
class SegTree{
private:
    vector <T> tree, tag;
    
    inline ll ls(ll p) {return p << 1;}
    inline ll rs(ll p) {return p << 1|1;}

    void push_up(ll p){
        tree[p] = tree[ls(p)] + tree[rs(p)];
    }

    void addtag(ll p, ll pl, ll pr, T d){
        tag[p] += d;
        tree[p] += (pr- pl + 1) * d;
    }

public:
    SegTree(int n){
        tree.resize(n << 2, 0);
        tag.resize(n << 2, 0);
    }

    void build(ll p, ll pl, ll pr){
        tag[p] = 0;
        if(pl == pr){
            tree[p] = ::a[pl];
            return;
        }
        ll mid = (pl + pr) >> 1;
        build(ls(p), pl, mid);
        build(rs(p), mid+1, pr);
        push_up(p);
    }

    void push_down(ll p, ll pl,ll pr){
        if(tag[p]){
            ll mid = (pl + pr) >> 1;
            addtag(ls(p), pl, mid, tag[p]);
            addtag(rs(p), mid+1, pr, tag[p]);
            tag[p] = 0;
        }
    }

    void update(ll L, ll R, ll p, ll pl, ll pr, T d){
        if(L <= pl && pr <= R){
            addtag(p, pl, pr, d);
            return;
        }
        push_down(p, pl, pr);
        ll mid = (pl + pr) >> 1;
        if(L <= mid) update(L, R, ls(p), pl, mid, d);
        if(R > mid) update(L, R, rs(p), mid+1, pr, d);
        push_up(p);
    }

    T query(ll L, ll R, ll p, ll pl, ll pr){
        if(pl >= L && pr <= R) return tree[p];
        push_down(p, pl, pr);
        ll mid = (pl + pr) >> 1;
        T res = 0;

        if(L <= mid) res += query(L, R, ls(p), pl, mid);
        if(R > mid) res += query(L, R, rs(p), mid+1, pr);

        return res;
    }

};


int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int n;
    cin >> n;
    for(int i=1;i<=n;i++){
        cin >> a[i];
    }
    SegTree <ll> sgt(n);
    sgt.build(1,1,n); //建树
    int l = 3, r = 3;
    sgt.update(l, r, 1, 1, n, 5); // 更新，区间[3,3]增加5
    sgt.query(1,n,1,1,n); //查询区间[1,n]的和
    return 0;
}

并查集

将编号分别为$1 \sim n$的$n$个对象划分为不相交集合，在每个集合中，选择其中某个元素代表所在集合。在这个集合中，并查集的操作有初始化，合并，查找。并查集操作的时间复杂度是$O(1)$的。

合并：合并两个元素所属集合（合并对应的树）

查询：查询某个元素所属集合（查询对应的树的根节点，也就是祖先），这可以用于判断两个元素是否属于同一集合

用并查集的基础操作完成HDU 1213

题目

代码

#include <bits/stdc++.h>
using namespace std;
int s[1005];

int find_s(int x){
    return (x==s[x] ? x:find_s(s[x]));
}

void union_s(int a,int b){
    int x=find_s(a),y=find_s(b);
    if(x!=y) s[x]=s[y];
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t;
    cin >> t;
    while(t--){
        int n,m,a,b,sum=0;
        cin >> n >> m;
        for(int i=0;i<1005;i++) s[i]=i;
        for(int i=1;i<=m;i++){
            cin >> a >> b;
            union_s(a,b);
        }
        for(int i=1;i<=n;i++)
            if(s[i]==i) sum++;
        cout << sum << '\n';
    }
    return 0;
}

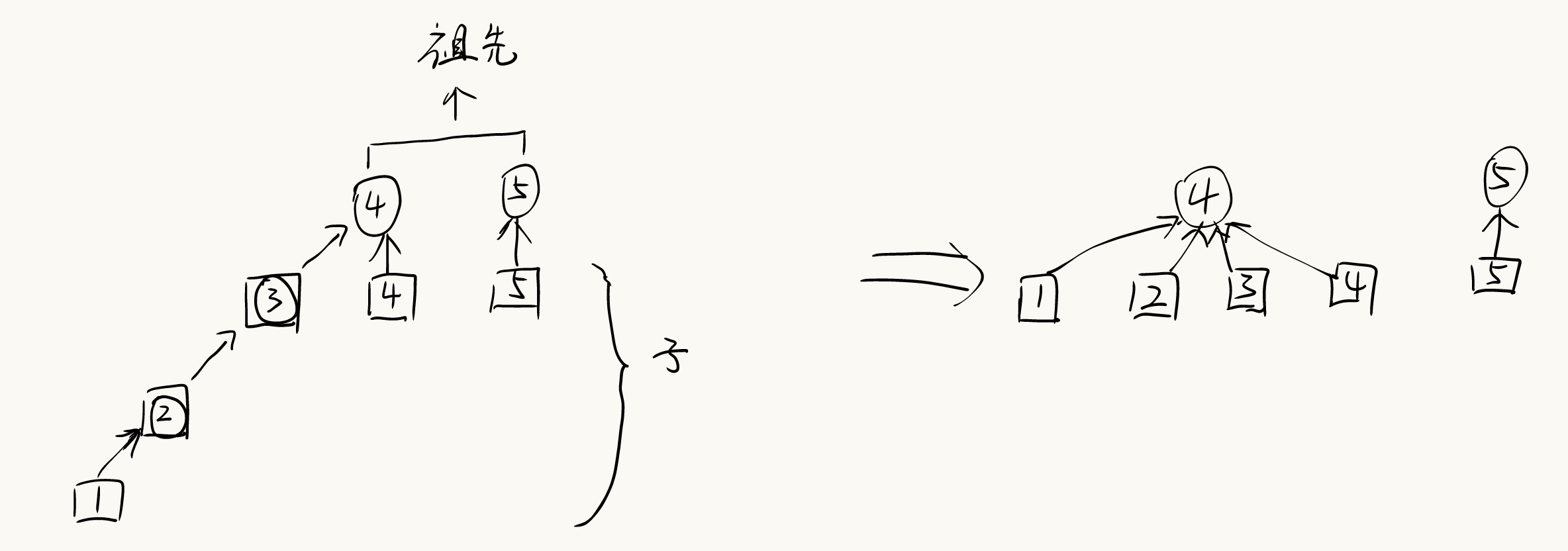
路径压缩

在合并过程中，树可能会发生退化，退成链表，增加查询的时间复杂度。通过路径压缩，将所有的子节点直接连到根节点，可大幅缩短搜索路径，加快查询，使树扁平化

int find_s(int x){
    return (x==s[x] ? x : s[x]=find_s(s[x]));
}

按秩合并

这是合并的优化，我们让小集合的根指向大集合的根，这样更好一些。定义size[i]为以$i$为根的集合的大小。

vector <int> siz(N,1);
void union_s(int x,int y){
    x = find_s(x), y = find_s(y);
    if(x == y) return;
    if(siz[x] > siz[y]) swap(x,y);
    s[x] = y;
    siz[y] += siz[x];
}

模板

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;

vector <int> s[maxn], siz(maxn,1);

void __init__(int n){
    for(int i = 1;i<=n;i++) s[i] = i;
}

int find_s(int x){
    return (x == s[x] ? x : s[x] = find_s(s[x]));
}

void union_s(int x,int y){
    x = find_s(x), y = find_s(y);
    if(x == y) return;
    if(siz[x] > siz[y]) swap(x,y);
    s[x] = y;
    siz[y] += siz[x];
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);

    return 0;
}

类版本模板

class dsu{
private: 
    vector<int> s, siz;
public:
    dsu(int n){
        s.resize(n+5);
        siz.assign(n+5,1);
        for(int i=1;i<=n;i++) s[i] = i;
    }

    int find_s(int x){
        return x = s[x] ? x : s[x] = find_s(s[x]);
    }

    void union_s(int x, int y){
        int x1 = find_s[x], y1 = find_s[y];
        if(x1 == y1) return;
        if(siz[x1] > siz[y1]) swap(x1,y1);
        s[x] = y;
        siz[y] += siz[x];
    }
};

LCA

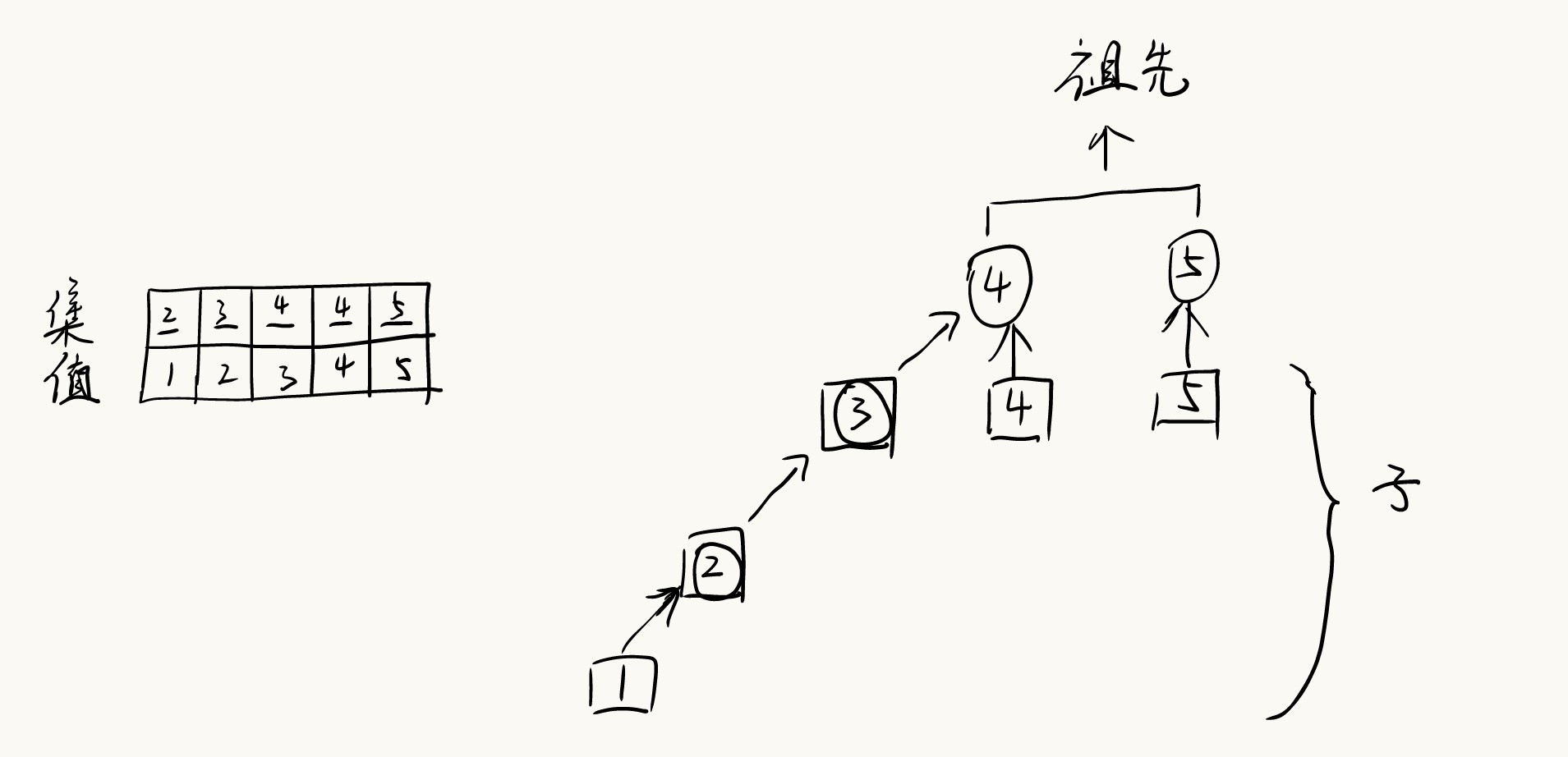
LCA(Lowest Common Ancestor)最近公共祖先，就是两个节点的公共祖先里面，离他们最近的那个祖先。

ST表倍增求解LCA

求解a，b两个点的LCA，你可能会想到暴力，这两个点一起，向它们的父节点跳，直到它们相遇，相遇的节点就是LCA。这种暴力的做法时间复杂度为$O(n)$，在竞赛中通常会TLE。

既然一步一步跳太慢，那么我们可以通过二进制拆分和倍增思想，一次跳一大步。在预处理之后，它能够一次性向上跳 $2^j$ （$j=0, 1, 2, ...$）步。预处理的时间复杂度为$O(nlogn)$

我们定义：$f[i][j]$ 表示：节点 i 向上跳 $2^j$ 步后到达的祖先节点 ， $d[i]$ 表示每个节点的深度。。

$f$数组的求得方法是

• 当 j = 0 时，fa[i][0] 就是 i 的父节点。
• 对于 j > 0，我们把"向上跳$2^i$步"拆成两半来跳，分解为：先从 i 向上跳 $2^{j-1}$ 步，到达节点 k；再从节点 k 向上跳 $2^{j-1}$ 步。

于是，我们就得到了状态转移方程：

$$fa[i][j] = fa[fa[i][j-1]][j-1]$$

这就是ST表的做法，通过二分、倍增的思想来优化区间查询，时间复杂度为$O(mlogn)$，m为查询次数。

总时间复杂度$O((n+m)logn)$。

以下是LCA模板题 洛谷P3379

---

P3379 【模板】最近公共祖先（LCA）

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入格式

第一行包含三个正整数 $N,M,S$，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来 $N-1$ 行每行包含两个正整数 $x, y$，表示 $x$ 结点和 $y$ 结点之间有一条直接连接的边（数据保证可以构成树）。

接下来 $M$ 行每行包含两个正整数 $a, b$，表示询问 $a$ 结点和 $b$ 结点的最近公共祖先。

输出格式

输出包含 $M$ 行，每行包含一个正整数，依次为每一个询问的结果。

输入输出样例 #1

输入 #1

5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5

输出 #1

4
4
1
4
4

说明/提示

对于 $30\%$ 的数据，$N\leq 10$，$M\leq 10$。

对于 $70\%$ 的数据，$N\leq 10000$，$M\leq 10000$。

对于 $100\%$ 的数据，$1 \leq N,M\leq 5\times10^5$，$1 \leq x, y,a ,b \leq N$，不保证 $a \neq b$。

---

以下是基于ST表的模板代码:

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ull = unsigned long long;
using pii = pair<int,int>;
using pll = pair<ll,ll>;
using pull = pair<ull,ull>;
using vec = vector<int>;
using vecl = vector<ll>; 
using maii = map<int,int>;
#define pb(x) push_back(x) 
#define eb(x) emplace_back(x)
const int maxn = 5e5+5;
int n, m, s, a, b;
vec e[maxn], d(maxn);
vector <vector<int>> f(maxn, vector<int>(25));

void dfs(int u,int father){
    d[u] = d[father] + 1;
    f[u][0] = father;
    for(int i=1;i<=20;i++)
        f[u][i] = f[f[u][i-1]][i-1];
    for(auto v:e[u])
        if(v != father) dfs(v,u);
}

int lca(int a, int b){
    if(d[a] < d[b]) swap(a, b);
    for(int i=20;~i;i--)
        if(d[f[a][i]] >= d[b]) a = f[a][i];
    if(a == b) return b;
    for(int i=20;~i;i--)
        if(f[a][i] != f[b][i]) a = f[a][i], b = f[b][i];
    return f[a][0];
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n >> m >> s;
    for(int i=1;i<n;i++){
        cin >> a >> b;
        e[a].eb(b), e[b].eb(a);
    }
    dfs(s, 0);
    for(int i=1;i<=m;i++){
        int x, y; cin >> x >> y;
        cout << lca(x, y) << '\n';
    }
    return 0;
}