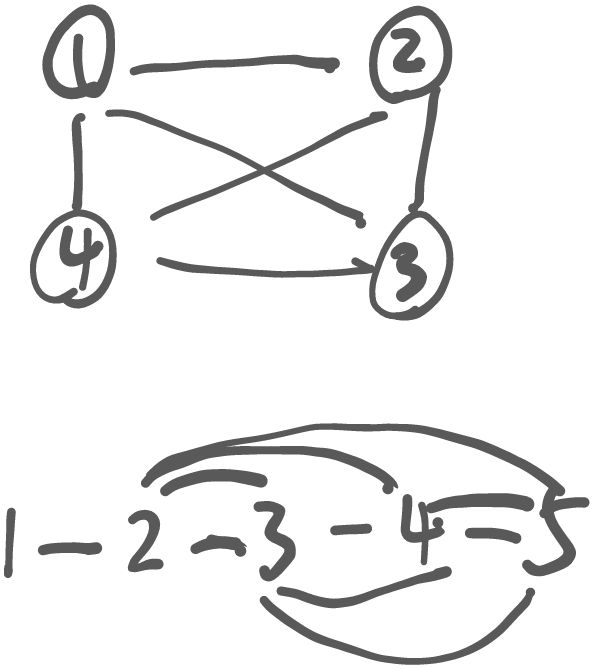概念与公式

完全图

完全图（Complete Graph）是一个简单的无向图，其中每一对不同的顶点之间都恰好有一条边相连。换句话说，完全图是一个所有顶点都相互连接的图。

完全图的性质包括：

顶点数为(n)的完全图有 $(\frac{n(n-1)}{2})$ 条边。
完全图中的每个顶点的度数都是(n-1)。
完全图是连通的，且是((n-1))-连通的。
完全图是((n-1))-正则的。
完全图(K_n)的色数是(n)，即需要(n)种颜色才能给图中的顶点着色，使得任何两个相邻的顶点颜色不同。

图的储存

邻接矩阵

用矩阵graph[N][N]储存边，N为节点总数。若 i 和 j 是直连的邻居，则用graph[i][j]表示边(i,j)的权值；若 i 和 j 不直连，一般把graph[i][j]复制无穷大。

邻接矩阵适合稠密图(大部分边都有权值)，不适合稀疏图(大部分边都无穷大)。

邻接矩阵的空间大小是N²。能表示有向边或无向边，若是无向图，那么边 i -> j 的权值是graph[i][j]=graph[j][i]；若是有向图，那么graph[i][j]是边 i -> j 的权值，graph[j][i]是边 j -> i 的权值。

邻接矩阵的优点：

简单直接，编程简单；
查找快，O(1)复杂度
适合稠密图

缺点：

表示稀疏图时十分浪费空间
边有多个权值时不能储存，即不能储存重边

邻接表

每个节点只储存它的直连邻居，一般用链表储存这些邻居，节省空间，存储效率高，存储复杂度为 $O(n+m)$ ，n为节点数量，m为边数，几乎达到了最优复杂度，而且能储存重边。缺点是找一个节点的邻居时，要逐个遍历它的邻接表。一般用vector实现。

struct edge{        //定义边
    int from, to, w;            //from是起点，to是终点，w是权值
    edge(int a,int b,int c){from = a,to = b,w = c;} //对边赋值
};
vector <edge> e[N];        //e[i]：存储第i个节点连接的所有边
//init
for(int i=1;i<=n;i++)
    e[i].clear();
//存边
e[a].push_back(edge(a,b,c));    //把(a,b)存到节点a的邻接表中
//遍历节点u的所有邻居
for(int i=0;i<e[u].size();i++){
//for(int v:e[u]) //上一行的简单写法
    int v = e[u][i].to, w = e[u][i].w;
}

拓扑排序

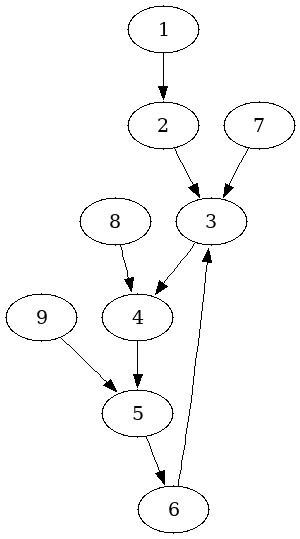
拓扑排序不是对数字进行大小排序的那种排序，而是对一系列事物的顺序关系和依赖关系进行排序，属于图论。拓扑排序的排序结果通常不是唯一的。

一个图能进行拓扑排序的充要条件是它是一个有向无环图(DAG)。

拓扑排序需要用到点的入度(Indegree)和出度 (Outdegree)

入度：以点 $v$ 为终点的边的数量，称为 $v$ 的入度。
出度：以点 $u$ 为起点的边的数量，称为 $u$ 的出度。

一个点的入度为0，说明它是起点，是排在最前面的；一个点的出度为0，说明它是终点，排在最后面。

拓扑排序的简单的图遍历，用BFS和DFS都能实现。

基于BFS的拓扑排序

(1)无前驱的顶点优先

先输出入度为0的点(无前驱，优先级最高)，以下是具体步骤：

找所有入度为0的点，放入队列作为起点，这些点谁先谁后没有关系。如果找不到入度为0的点，说明这个图不是DAG，不存在拓扑排序。
弹出队首元素a，将a的所有邻居点入度-1，入度减为0的邻居点入队。没有减为0的不入队。
继续上述操作，直到队列为空为止。队列的输出就是一个拓扑排序。

拓扑排序无解的判断(找环)：

如果队列已空，但是还有点未入队，那么这些点的入度都不为0，说明图不是DAG，不存在拓扑排序。这也说明图上存在环，可以用来找环，没有进入队列的点，就是环上的点。

(2)无后驱的顶点优先

和无前驱反过来就行，先找出度为0的点。

BFS的时间复杂度为 $O(n+m)$ ，其中m为入度为0的点。

基于DFS的拓扑排序

DFS很适合拓扑排序。

一个有向无环图，从一个入度为0的点 $u$ 开始DFS，DFS递归返回的顺序就是拓扑排序(是一个逆序)。DFS递归返回的首先是最底层的点，它一定是出度为0的点；然后逐步回退，最后输出起点 $u$ 。

如果图是有环图，则不存在拓扑排序，那么在递归时，会出现回退边。在代码中这样发现回退边：记录每个点的状态，如果dfs递归到某个点时发现它仍在前面的递归中没有处理完毕，说明存在回退边，不存在拓扑排序。

例题POJ 1270

#include <bits/stdc++.h>
using namespace std;
#define check (s[i]>='a' && s[i]<='z')
const int maxn = 30;

int n,in[maxn],a[maxn],topo[maxn];
bool link[maxn][maxn],vis[maxn];

void dfs(int u,int cnt){
    topo[cnt] = u;
    if(cnt == n-1){
        for(int i=0;i<n;i++) cout << char('a'+topo[i]) << ' ';
        cout << '\n';
        return;
    }
    vis[u] = 1;
    for(int i=0;i<n;i++){
        if(!vis[a[i]] && link[u][a[i]])
            in[a[i]]--;
    }
    for(int i=0;i<n;i++){
        if(!vis[a[i]] && !in[a[i]])
            dfs(a[i],cnt+1);
    }
    for(int i=0;i<n;i++){
        if(!vis[a[i]] && link[u][a[i]])
            in[a[i]]++;
    }
    vis[u] = 0;
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    string s;
    while(getline(cin,s)){
        memset(in,0,sizeof(in));
        memset(link,0,sizeof(link));
        memset(vis,0,sizeof(vis));
        int len = s.size();
        n = 0;
        for(int i=0;i<len;i++)
            if(check) a[n++] = s[i]-'a';
        sort(a,a+n);
        getline(cin,s);
        len = s.size();
        int f = 1,st,ed;
        for(int i=0;i<len;i++){
            if(f && check){
                f = 0;
                st = s[i] - 'a';
                continue;
            }
            if(!f && check){
                f = 1;
                ed = s[i] - 'a';
                link[st][ed] = 1;
                in[ed]++;
                continue;
            }
        }
        for(int i=0;i<n;i++){
            if(!in[a[i]])
                dfs(a[i],0);
        }
        cout << '\n';
    }
    return 0;
}

基环树

基环树不是树，而是只有一个连通环的图，它有 $n$ 个点和 $n$ 条边。

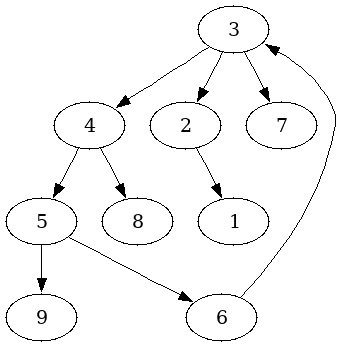
无向图上的基环树。在一颗基于无向图的无根树加上一条边，就形成了基环树。去掉环上任意一条边，基环树就变成了一颗真正的树
有向图上的基环树。一个有向无环图，如果能在图中加一条边形成一个自连通的环，则形成一颗基环树。把环看成一个整体，根据它与环外点的关系，把基环树分为两种：内向树，环外的点只能进入环内，所有边都指向环；外向树，环外的点无法进入环内，所有边都背离环。

（图是丑了一点，意思到位就行…）

基环树的找环问题，就是“图的连通性”的一个简化问题。

无向图，用拓扑排序的BFS找出环，操作结束后，度数大于 $1$ 的点就是环上的点。
具体做法：①计算所有点的度数；②把所有度数为 $1$ 的点入队；③队列弹出度数为1的点，把它连的所有边都去掉，并将边所连的邻居点的度数减 $1$ ，如果这个邻居的度数变为 $1$ 就入队；④重复以上操作，直到队列为空。操作结束后，统计度数大于 $1$ 的点，就是环上的点。(这种找环的方法只适用于只有一个环的基环树)

找环上的一点，用DFS可以方便的找到：如果一个点 $v$ 第二次被访问，那么就存在环，且 $v$ 在环上。这个方法同时适用于有向图和无向图。

看一道例题：洛谷P2607

树形DP+基环树

骑士之间的关系构成了基环树森林。并且这道题从任意一个节点出发，一定可以找到一个环。所以解体主要是找到一个环，并用mark记录环上一点，把这个点的一条边断开，然后分别在父节点和子节点上做树上DP，取最大值；再去找其它没有访问过的环重复操作。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int maxn = 1e6+5;

class node{
    public:
        int father,val;
}p[maxn];

vector <int> G[maxn];
int n,mark;
bool vis[maxn];
ll dp[maxn][2];

void add(int i,int f,int v){
    G[f].push_back(i);
    p[i] = {f,v};
}

int findp(int u){
    vis[u] = 1;
    int f = p[u].father;
    if(vis[f]) return f;
    else return findp(f);
}

void dfs(int u){
    dp[u][0] = 0;
    dp[u][1] = p[u].val;
    vis[u] = 1;
    for(auto v:G[u]){
        if(v == mark) continue;
        dfs(v);
        dp[u][1] += dp[v][0];
        dp[u][0] += max(dp[v][0],dp[v][1]);
    }
}

ll solve(int u){
    ll res = 0;
    mark = findp(u);
    dfs(mark);
    res = max(res,dp[mark][0]);
    mark = p[mark].father;
    dfs(mark);
    res = max(res,dp[mark][0]);
    return res;
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n;
    for(int i=1;i<=n;i++){
        int v,f;
        cin >> v >> f;
        add(i,f,v);
    }
    ll ans = 0;
    for(int i=1;i<=n;i++){
        if(!vis[i]) ans += solve(i);
    }
    cout << ans << '\n';
    return 0;
}