组合数学

---

容斥原理

集合 $S$ 的子集 $A_1$ 有性质 $p_1$ ，$A_2$ 有性质 $P_2$ ， $\dots$ ， $A_n$ 有性质 $P_n$ 。
那么，集合 $S$ 中具有性质 $P_1,P_2,\dots,P_n$ 的集合个数为

$$\Big|\bigcap_{i=1}^nA_i \Big| = \sum_{i=1}^n\left| A_i\right| - \sum_{1 \leq i \leq j \leq n} \left| A_i \cap A_j \right| + \sum_{1 \leq i \leq j \leq k \leq n} \left| A_i \cap A_j \cap A_k \right| - \dots + (-1)^{n+1} \left| \cap_{i=1}^n A_i \right|$$

那么不具有性质 $P_1,P_2,\dots,P_n$ 的集合个数呢？很明显就是

$$\Big| S \Big| - \Big| \bigcap_{i=1}^n A_i \Big|$$

---

来个例子加深理解

问题：在100人中，60人喜欢咖啡，40人喜欢茶，20人两者都喜欢。求至少喜欢一种饮料的人数？一种饮料都不喜欢的人数？

解答：
设 $A$ 为喜欢咖啡的集合，$B$ 为喜欢茶的集合。
容斥原理给出：

$$|A \cup B| = |A| + |B| - |A \cap B| = 60 + 40 - 20 = 80.$$

因此，80人喜欢至少一种饮料。

$$|\complement_S A| = |S| - |A \cup B| = 100 - 80 = 20.$$

因此，20人一种饮料都不喜欢

---

以下是一道例题(2024CCPC新疆E题):

---

题目

Bob现在具有一个长为 $n$ 的序列 $a_1,a_2,a_3,\cdots,a_n$。

一共有 $q$ 次询问，每次给定一个数 $x$。

询问在 $[1,x]$ 中有多少个 正整数 满足它不是任何 $a_i$ 的倍数。

输出满足这样要求的正整数数量。

输入

第一行一个正整数 $n$，表示数组的长度。

第二行 $n$ 个正整数，第 $i$ 个正整数表示 $a_i$。

第三行一个正整数 $q$，表示共有$q$个询问。

接下来的 $q$ 行中，第 $i$ 行一个正整数 $x$ 表示当次询问。

其中保证$n \leq 10,q \leq 10^4, a_i, x \leq10^9$.

---

子集共有 $2^n$ 个，用二进制法把每个子集给枚举出来，奇数个子集相加，偶数个子集减去，本题属于"不是、不具有"的情况，因此满足“不具有”的情况就是总集减去子集数

#include <bits/stdc++.h>
using namespace std;
using ull = unsigned long long;

int n,q,a[15];

inline ull lcm(int x,int y){
    return x/__gcd(x,y)*y;
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n;
    for(int i=1;i<=n;i++){
        cin >> a[i];
    }
    cin >> q;
    while(q--){
        ull x, ans = 0; 
        cin >> x;
        for(int i = 1; i < (1 << n); i++){
            ull sum = 0, glcm = 1;
            for(int j=0;j<n;j++){
                if((i>>j) & 1){
                    sum++;
                    glcm = lcm(glcm,a[j+1]);
                }
            }
            if(sum & 1) ans += x/glcm;
            else ans -= x/glcm;
        }
        cout << x - ans << '\n';
    }
    return 0;
}

---

鸽巢原理

鸽巢原理,即抽屉原理,其主要内容是: 把 n+1 个物体放进 n 个盒子,至少有一个盒子包含两个或更多物体.

题目

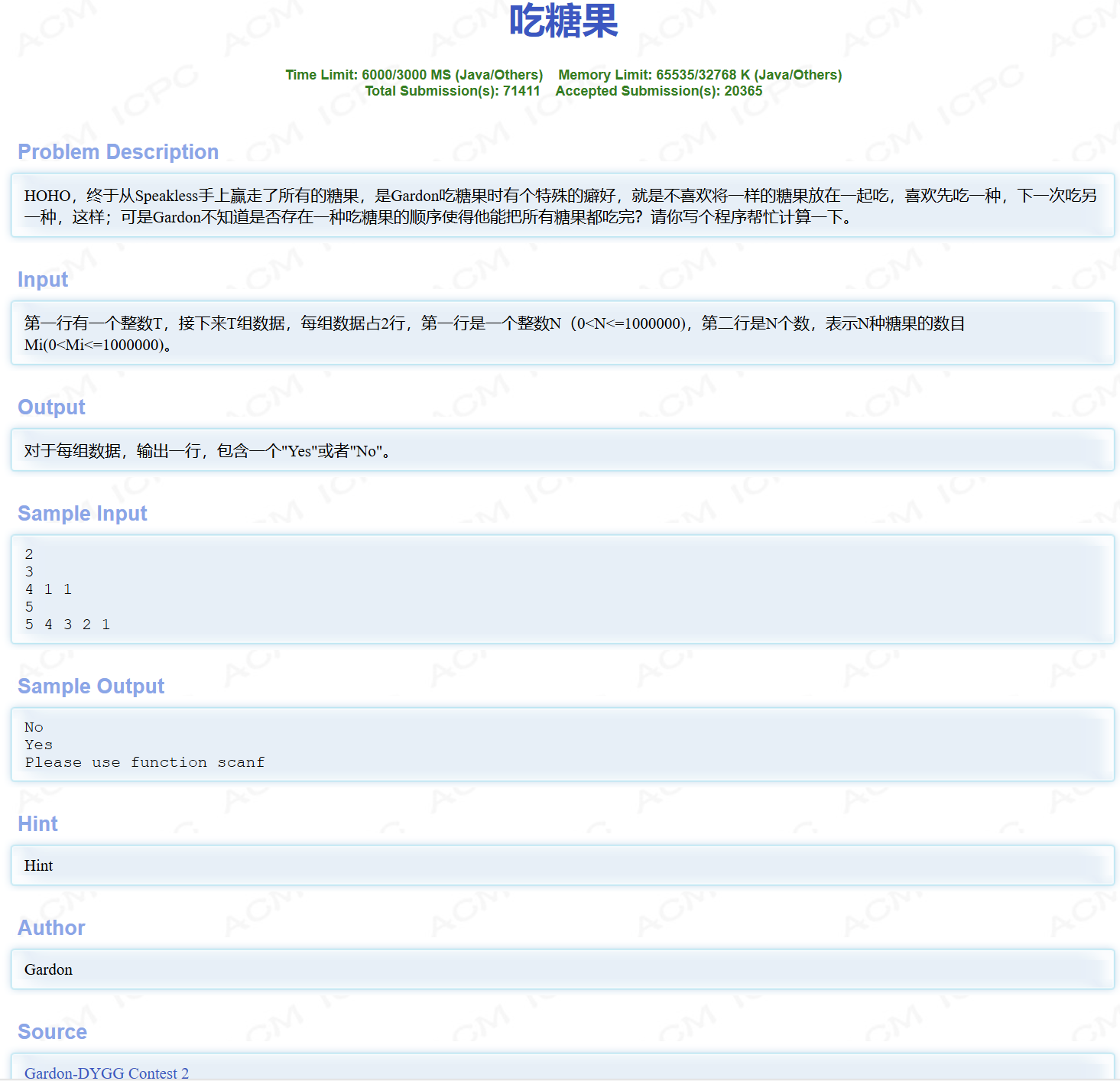
以HDU 1205举例

这题如果去模拟的话还是比较麻烦,但是如果用鸽巢原理就很简单.

隔板法: 找出最多数量的那种糖果, 把它看成n个隔板,每个隔板的右边放置其他糖果.

令其他糖果总数为s,

如果 s< n-1 ,一定无解,这会使两个隔板之间没有其他糖果

如果 s>= n-1,一定有解,因为隔板的数量比剩下每种糖果的数量都多,因此不会有相邻同种糖果.

(看似简单的一题通过率仅28.5% , 这题有坑! 可能出现1e6 * 1e6的情况 , 不得不#define int long long)

代码

#include <bits/stdc++.h>
using namespace std;
#define int long long

signed main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t,n;
    cin >> t;
    while(t--){
        cin >> n;
        int mx=0,s=0,ai;
        for(int i=0;i<n;i++){
            cin >> ai;
            mx=max(mx,ai);
            s+=ai;
        }
        s-=mx;
        cout << ((s<mx-1)?"No\n":"Yes\n");
    }
    return 0;
}

---