树形DP

首先是树的储存，树的储存是图的储存的特殊情况，可以用邻接表储存，或链式向前星

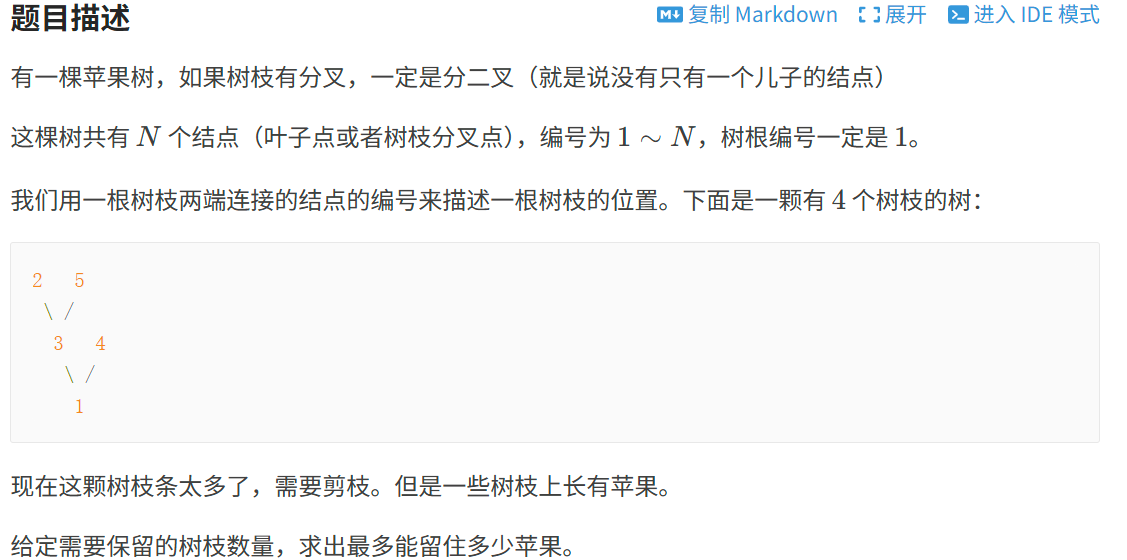
洛谷P2015二叉苹果树

定义状态dp[u][j]表示以节点u为根的子树上留 j 条边时的最多苹果数量。dp[1][q]就是答案。

状态转移方程：dp[u][j] = max(dp[u][j], dp[u][j-k-1] + dp[v][k] + w)

其中，v 是 u 的一个子节点。dp[u][j]的计算分以下两部分：

  1. dp[v][k]：在v上留k条边
  2. dp[u][j-k-1]：除了v上的k条边，以及u-v边，那么以u为根的这棵树上还有j-k-1条边，它们在u的其他子节点上

总复杂度小于O(n3)

PS：

  1. 这道题是无向图储存，因为题目没有说明输入的两个节点哪个是爹哪个是儿，所以要push_back两次，然后在搜的时候跳过father
  2. j 循环必须递减，例如dp[u][5]会用到dp[u][4]和dp[u][3]等等，若是递减循环，先算5，再算4，再算3…dp[u][5]用到的是dp[u][4]和dp[u][3]的原值；若是递增循环，dp[u][5]就会用到dp[u][4]和dp[u][3]的新计算后的值，就不对了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <bits/stdc++.h>
using namespace std;
const int N = 200;
int n,q;
int dp[N][N], sum[N];    //sum[i]记录以[i]为根的子树的总边数

struct node{
    int v,w;			//v是子节点，w是边u-v的权值
    node(int a,int b) : v(a),w(b) {}
};
vector <node> e[N];

void dfs(int u,int father){
    for(auto i:e[u]){	//用i遍历u的所有子节点
        if(i.v == father) continue;	//不回头搜父亲，避免循环
        dfs(i.v,u);	//递归到最深的叶子节点，然后返回
        sum[u] += sum[i.v]+1;	//子树上的总边数
        /*两个for循环这样写简单，就是没有优化
        for(int j=sum[u];j>=0;j--)
            for(int k=0;k<=j-1;k++)
        */
        for(int j=min(q,sum[u]);j>=0;j--)
            for(int k=0;k<=min(sum[i.v],j-1);k++)
                dp[u][j] = max(dp[u][j], dp[u][j-k-1] + dp[i.v][k] + i.w);
    }
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n >> q;
    for(int i=1;i<n;i++){
        int u,v,w;
        cin >> u >> v >> w;
        e[u].push_back({v,w});
        e[v].push_back({u,w});	//无向边
    }
    dfs(1,0);
    cout << dp[1][q];
    return 0;
}

没有上司的舞会

典，上图


这题和上题有点区别

这题没有定义结构体，因为这题是有向无权图，题目已经表明了输入的节点中哪个是爹哪个是儿，而且没有边上没有权值。

定义状态dp[u][0]表示不选择当前节点的最优解，dp[u][1]表示选择当前节点的最优解。

状态转移方程：
dp[u][1] += dp[v][0];选择该节点，就累加上不选子节点的最大值

dp[u][0] += max(dp[v][0], dp[v][1]);不选该节点，子节点可选可不选

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <bits/stdc++.h>
using namespace std;
const int N = 6666;
int n, dp[N][2], w[N], father[N];
vector <int> e[N];

void dfs(int u){
    dp[u][0] = 0;
    dp[u][1] = w[u];
    for(auto v:e[u]){
        dfs(v);
        dp[u][1] += dp[v][0];
        dp[u][0] += max(dp[v][0], dp[v][1]);
    }
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n;
    for(int i=1;i<=n;i++) cin >> w[i];
    for(int i=1;i<n;i++){
        int u,v;
        cin >> v >> u;
        e[u].push_back(v);
        father[v] = u;
    }
    int t = 1;
    while(father[t]) t = father[t];
    dfs(t);
    cout << max(dp[t][0], dp[t][1]) << '\n';
    return 0;
}

战略游戏

树上DP，和舞会差不多，拿来练熟练度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1505;

int dp[maxn][2];
vector <int> e[maxn];

void dfs(int u,int father){
    dp[u][0] = 0;
    dp[u][1] = 1;
    for(auto i:e[u]){
        if(i == father) continue;
        dfs(i,u);
        dp[u][0] += dp[i][1];
        dp[u][1] += min(dp[i][0],dp[i][1]); 
    }
}
int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int n;
    cin >> n;
    for(int i=1;i<=n;i++){
        int a,b,c;
        cin >> a >> b;
        for(int j=0;j<b;j++){
            cin >> c;
            e[a].push_back(c);
            e[c].push_back(a);
        }
    }
    dfs(0,-1);
    cout << min(dp[0][0],dp[0][1]) << '\n';
    return 0;
}

Dijkstra

迪杰斯特拉简单概括为 BFS+贪心。适合单源最短路。注意，dijkstra不能做边权为负数的题目。

模板题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <bits/stdc++.h>
using namespace std;
const long long INF = 0x3f3f3f3f3f3f3f3fLL; //这样定义的好处是INF <= INF+x 
const int N = 3e5+2;

struct edge{
    int from, to; //边：起点，终点，权值；起点from并没有用到，e[i]的i就是from 
    long long w; //权值 
    edge(int a,int b,long long c) : from(a),to(b),w(c) {}
};

vector <edge> e[N];  //邻接表存图 

struct node{
    int id; long long n_dis; //id：节点；n_dis：这个节点到起点的距离 
    node(int b,long long c){id = b;n_dis = c;}
    bool operator < (const node & a) const 
    {return n_dis > a.n_dis;}
};

int n,m;
int pre[N]; //记录前驱节点 

void print_path(int s,int t){ //打印s到t的最短路径 
    if(s == t) {cout << s << '\n';return;} //打印起点 
    print_path(s,pre[t]); //先打印前一个点 
    cout << t << '\n'; //后打印当前点，最后打印终点t 
}

long long dis[N]; //记录所有节点到起点的距离 
bool done[N]; //true表示节点i已经访问过 

void dijkstra(){
    int s = 1; //起点s=1 
    for(int i=1;i<=n;i++){dis[i] = INF;done[i] = false;} //初始化 
    dis[s] = 0; //起点到自己的距离为0 
    priority_queue <node> q; //优先队列，存节点信息
    q.push({s,dis[s]});
    while(!q.empty()){
        node u = q.top(); //弹出离起点s距离最小的点u 
        q.pop();
        if(done[u.id]) continue;
        done[u.id] = true;
        for(edge v:e[u.id]){ //访问节点u的所有邻居 
            if(done[v.to]) continue;
            if(dis[v.to] > u.n_dis + v.w){  
                dis[v.to] = u.n_dis + v.w;
                q.push({v.to,dis[v.to]}); //拓展新邻居，加入队列 
                pre[v.to] = u.id; //记录新邻居v的前驱为u 
            }
        }
    }
    //print_path(s,n) 	//如有需要就打印s到n的最短路径 
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n >> m;
    for(int i=0;i<m;i++){
        int u,v,w;
        cin >> u >> v >> w;
        e[u].push_back({u,v,w});
        //e[v].push_back({u,w});	//这道模板题是单向边 
    }
    dijkstra();
    for(int i=1;i<=n;i++){
        if(dis[i]>=INF) cout << "-1 ";
        else cout << dis[i] << ' ';
    }
    cout << '\n';
    return 0;
}

PTA

L1-006

这道题是L1里面的难题了，比一些L2的都难

由于13！超int了，所以从能分解出13个因子开始，递减枚举，这样可以保证第一个枚举出来的因子分解长度是最长的

然后起始因子从2到n/j逐个枚举(之所以是n/j，是因为j最大就是sqrt(n))

当n%temp==0就停止了，这里是贪心，因为i的递减枚举保证因子序列长度最长，j的递增枚举保证因子序列字典序最小，当碰到第一个满足条件的因子序列时，不用多想，答案就是它！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <bits/stdc++.h>
#define int long long
using namespace std;

signed main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int n;
    cin >> n;
    for(int i=13;i>=1;i--){
        for(int j=2;j<=n/j;j++){
            int temp = 1;
            for(int k=0;k<i;k++){
                temp *= (j+k);
                if(temp > n) break;
            }
            if(temp > n) break;
            if(n % temp == 0){
                cout << i << '\n';
                for(int k=0;k<i;k++){
                    if(k==0) cout << j+k;
                    else cout << '*' << j+k;
                }
                cout << '\n';
                return 0;
            }
        }
    }
    cout << "1\n" << n << '\n';
    return 0;
}

L1-025

来感受一下天梯赛非人类的输入输出吧！这题就把这种恶心人的设定具象化了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <bits/stdc++.h>
using namespace std;

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    string s1,s2;
    cin >> s1;
    getline(cin,s2);
    
    bool pd1 = 1, pd2 = 1;
    int num1 = 0, num2 = 0, times1 = 1, times2 = 1;
    for(auto i:s1){
        if(i-'0'<0 || i-'0'>9){
            pd1 = 0;
            break;
        }
    }
    if(pd1){
        int si = s1.size();
        for(int i=si-1;i>=0;i--){
            num1 += (s1[i]-'0')*times1;
            times1 *= 10;
        }
    }
    for(int i=1;i<s2.size();i++){
        if(s2[i]-'0'<0 || s2[i]-'0'>9){
            pd2 = 0;
            break;
        }
    }
    if(pd2){
        int si = s2.size();
        for(int i=si-1;i>=1;i--){
            num2 += (s2[i]-'0')*times2;
            times2 *= 10;
        }
    }
    if(pd1 && (num1<1 || num1>1000)) pd1=0;
    if(pd2 && (num2<1 || num2>1000)) pd2=0;
    if(pd1) cout << num1;
    else cout << '?';
    cout << " + ";
    if(pd2) cout << num2;
    else cout << '?';
    cout << " = ";
    if(pd1&&pd2) cout << num1+num2;
    else cout << '?';
    cout << '\n';
    return 0;
}

L1-103

模拟，本来是没什么难度的，但是被坑到了…还好是ioi，发现有一个test没过之后立马就发现错在哪了，不像某某赛制 自己怎么si的都不知道

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <bits/stdc++.h>
#define int long long
//其实应该是不会爆int的 
using namespace std;

bool cpa(pair<int,int> a, pair<int,int> b){
    if(a.first == b.first) return a.second < b.second;
    else return a.first > b.first;
}

int solve(int num){
    int cnt = 0,temp=1;
    while(num >= 10){
        while(num>0){
            temp *= num%10;
            num /= 10;
        }
        num = temp;
        temp = 1;
        cnt++;
    }
    return cnt;
}

signed main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int a,b,cnt=0;
    pair <int,int> arr[1001];
    cin >> a >> b;
    for(int i=a;i<=b;i++)
        arr[cnt++] = {solve(i),i};
    sort(arr,arr+1001,cpa);
    int maxn = arr[0].first;
    if(maxn == 0){
        cout << "0\n";
        for(int i=a;i<=b;i++){
            if(i==a) cout << i;
            else cout << ' ' << i;
        }
        return 0;
    }
    cout << maxn << '\n' << arr[0].second;
    for(int i=1;i<1001;i++){
        if(arr[i].first == maxn)
            cout << ' ' << arr[i].second;
        else break;
    }
    return 0;
}

L1-104

模拟，不需要动脑，纯模拟，cv工程师

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
#include <bits/stdc++.h>
#define int long long
#define check (a[i][j]<1 || a[i][j]>9 || num[a[i][j]])
using namespace std;
int t,a[10][10],num[10];

void solve(){
    for(int i=1;i<=9;i++)
        for(int j=1;j<=9;j++)
            cin >> a[i][j];
    for(int i=1;i<=9;i++){
        memset(num,0,sizeof(num));
        for(int j=1;j<=9;j++){
            if(check){
                cout << "0\n";
                return;
            }
            num[a[i][j]] = 1;
        }
    }
    for(int i=1;i<=9;i++){
        memset(num,0,sizeof(num));
        for(int j=1;j<=9;j++){
            if(a[j][i]<1 || a[j][i]>9 || num[a[j][i]]){
                cout << "0\n";
                return;
            }
            num[a[j][i]] = 1;
        }
    }
    memset(num,0,sizeof(num));
    for(int i=1;i<=3;i++){
        for(int j=1;j<=3;j++){
            if(check){
                cout << "0\n";
                return;
            }
            num[a[i][j]] = 1;
        }
    }
    memset(num,0,sizeof(num));
    for(int i=4;i<=6;i++){
        for(int j=1;j<=3;j++){
            if(check){
                cout << "0\n";
                return;
            }
            num[a[i][j]] = 1;
        }
    }
    memset(num,0,sizeof(num));
    for(int i=7;i<=9;i++){
        for(int j=1;j<=3;j++){
            if(check){
                cout << "0\n";
                return;
            }
            num[a[i][j]] = 1;
        }
    }
    memset(num,0,sizeof(num));
    for(int i=1;i<=3;i++){
        for(int j=4;j<=6;j++){
            if(check){
                cout << "0\n";
                return;
            }
            num[a[i][j]] = 1;
        }
    }
    memset(num,0,sizeof(num));
    for(int i=1;i<=3;i++){
        for(int j=7;j<=9;j++){
            if(check){
                cout << "0\n";
                return;
            }
            num[a[i][j]] = 1;
        }
    }
    memset(num,0,sizeof(num));
    for(int i=4;i<=6;i++){
        for(int j=4;j<=6;j++){
            if(check){
                cout << "0\n";
                return;
            }
            num[a[i][j]] = 1;
        }
    }
    memset(num,0,sizeof(num));
    for(int i=4;i<=6;i++){
        for(int j=7;j<=9;j++){
            if(check){
                cout << "0\n";
                return;
            }
            num[a[i][j]] = 1;
        }
    }
    memset(num,0,sizeof(num));
    for(int i=7;i<=9;i++){
        for(int j=4;j<=6;j++){
            if(check){
                cout << "0\n";
                return;
            }
            num[a[i][j]] = 1;
        }
    }
    memset(num,0,sizeof(num));
    for(int i=7;i<=9;i++){
        for(int j=7;j<=9;j++){
            if(check){
                cout << "0\n";
                return;
            }
            num[a[i][j]] = 1;
        }
    }
    cout << "1\n";
    return;
}

signed main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> t;
    while(t--){
        solve();
    }
    return 0;
}

L2-002

模拟链表，模拟好烦

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+1;
int n;
string ad1, start;

struct node{
    string sd;
    int sec;
    string ed;
};
map <string,int> ma;
vector <node> inp,outp,shan;
bool vis[maxn];

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> ad1 >> n;
    for(int i=0;i<n;i++){
        string sd,ed;
        int sec;
        cin >> sd >> sec >> ed;
        if(sd == ad1){
            start = ed;
            outp.push_back({sd,sec,ed});
            vis[abs(sec)] = 1;
        }
        ma[sd] = i;
        inp.push_back({sd,sec,ed});
    }
    while(start != "-1"){
        int index = ma[start];
        if(vis[abs(inp[index].sec)]){
            shan.push_back({inp[index].sd,inp[index].sec,inp[index].ed});
        }
        else{
            outp.push_back({inp[index].sd,inp[index].sec,inp[index].ed});
            vis[abs(inp[index].sec)] = 1;
        }
        start = inp[index].ed;
    }
    int si = outp.size();
    for(int i=0;i<si;i++){
        if(i!=si-1) outp[i] = {outp[i].sd,outp[i].sec,outp[i+1].sd};
        else outp[i] = {outp[i].sd,outp[i].sec,"-1"};
        cout << outp[i].sd << ' ' << outp[i].sec << ' ' << outp[i].ed << '\n';
    }
    si = shan.size();
    for(int i=0;i<si;i++){
        if(i!=si-1) shan[i] = {shan[i].sd,shan[i].sec,shan[i+1].sd};
        else shan[i] = {shan[i].sd,shan[i].sec,"-1"};
        cout << shan[i].sd << ' ' << shan[i].sec << ' ' << shan[i].ed << '\n';
    }
    return 0;
}

L2-003

第一眼：这题能放L2？这题L1的吧

第一次提交WA：哦，保留两位小数

第二次提交WA：哦，输入的可能是小数

第三次提交WA：哦，还有供不应求的情况

然后AC。。。总算知道这题为什么放L2了。。。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <bits/stdc++.h>
using namespace std;

bool cpa(pair<double,int> a,pair<double,int> b){
    return a.first > b.first;
}
int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int n,d;
    double a[1001],b[1001];
    pair <double,int> c[1001];
    cin >> n >> d;
    for(int i=0;i<n;i++) cin >> a[i];
    for(int i=0;i<n;i++){
        cin >> b[i];
        c[i] = {1.0*b[i]/a[i],a[i]};
    }
    sort(c,c+n,cpa);
    double sum = 0;
    int i = 0;
    while(d>0 && i<n){
        if(c[i].second <= d)
            sum += c[i].first * c[i].second;
        else
            sum += c[i].first * d;
        d -= c[i++].second;
        //cout<<i<<' '<<c[i].first<<'\n';
    }
    cout << fixed << setprecision(2) << sum << '\n';
    return 0;
}

L2-004

数据结构…临时学的…听说天梯赛常考树…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1008;

int n,ans1[maxn],ans2[maxn],c1=0,c2=0,inp[maxn];

bool check1(int l,int r){
    int x = inp[l];
    if(l>r) return 1;
    if(l==r){
        ans1[c1++] = x;
        return 1;
    }
    int i;
    for(i=l+1;i<=r && inp[i]<x;i++);
    i--;
    int j;
    for(j=i+1;j<=r && inp[j]>=x;j++);
    j--;
    if(j!=r) return 0;
    bool pd = check1(l+1,i) && check1(i+1,r);
    ans1[c1++] = x;
    return pd;
}

bool check2(int l,int r){
    int x = inp[l];
    if(l>r) return 1;
    if(l==r){
        ans2[c2++] = x;
        return 1;
    }
    int i;
    for(i=l+1;i<=r && inp[i]>=x;i++);
    i--;
    int j;
    for(j=i+1;j<=r && inp[j]<x;j++);
    j--;
    if(j!=r) return 0;
    bool pd = check2(l+1,i) && check2(i+1,r);
    ans2[c2++] = x;
    return pd;
}
int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n;
    for(int i=0;i<n;i++) cin >> inp[i];
    if(check1(0,n-1)){
        cout << "YES\n";
        for(int i=0;i<c1;i++){
            if(i) cout << ' ';
            cout << ans1[i];
        }
        cout << '\n';
    }
    else if(check2(0,n-1)){
        cout << "YES\n";
        for(int i=0;i<c2;i++){
            if(i) cout << ' ';
            cout << ans2[i];
        }
        cout << '\n';
    }
    else cout << "NO\n";
    return 0;
}