codeforces 991 div.3
A
题目
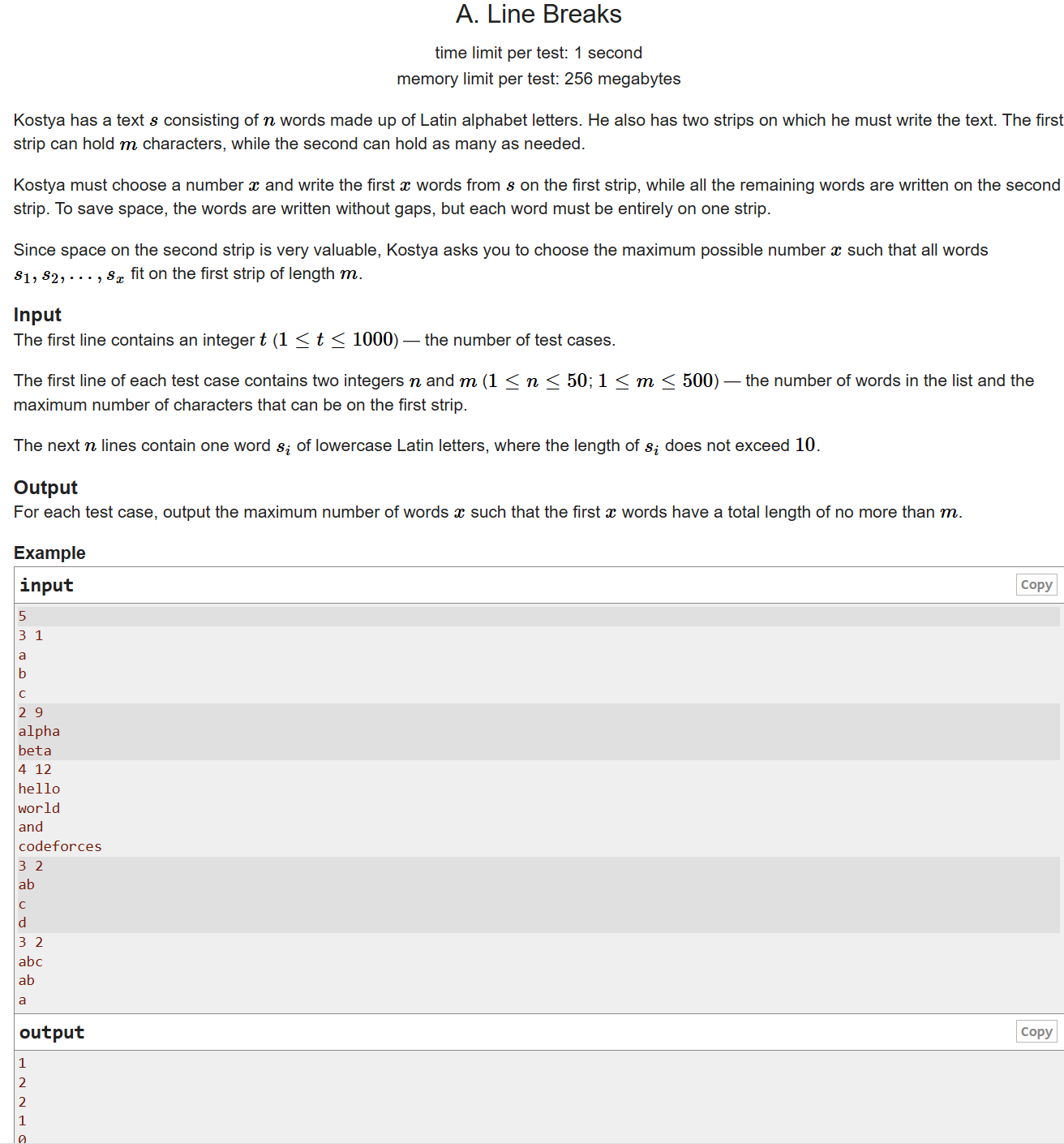
字符串处理,题意大概是:给你一个数字,问你有多少个完整的单词的字母数之和不超过这个数字。很简单的字符串题,运用字符串的size()函数即可。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| #include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n,m,sum=0;
string s;
cin >> n >> m;
while(n--){
cin >> s;
int len = s.size();
m-=len;
if(m>=0){
sum++;
}
}
cout << sum << '\n';
}
return 0;
}
|
B
题目

给你一个数组,让你在数组中出去第一个和最后一个数,剩下的数中选则一个数,并做以下操作之一:
- 该数的前一个数减一,后一个数加一
- 该数的前一个数加一,后一个数减一
问你在做n次操作后,能不能使得这个数组中所有数都相同
思考后发现,这些操作是有规律的,所有的操作都可以分为这两类:
- 奇数项进行数字加减
- 偶数项进行数字加减
我们只要判断:
- 所有数的和是否能整除n (因为数组最后全为n)
- 奇数项之和能否整除奇数的项数
- 偶数项之和能否整除偶数的项数
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 2e5;
int a[maxn+1];
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
memset(a,0,maxn+1);
int n,n_ji=0,sum=0,sum_ji=0,sum_ou=0;
cin >> n;
for(int i=0;i<n;i++){
cin >> a[i];
sum+=a[i];
if((i+1)%2){
sum_ji +=a[i];
n_ji++;
}
else sum_ou +=a[i];
}
if(sum%n){
cout << "NO\n";
continue;
}
int ave = sum/n;
if(sum_ji/n_ji != ave || sum_ou/(n-n_ji) != ave)
cout << "NO\n";
else cout << "YES\n";
}
return 0;
}
|
C
题目
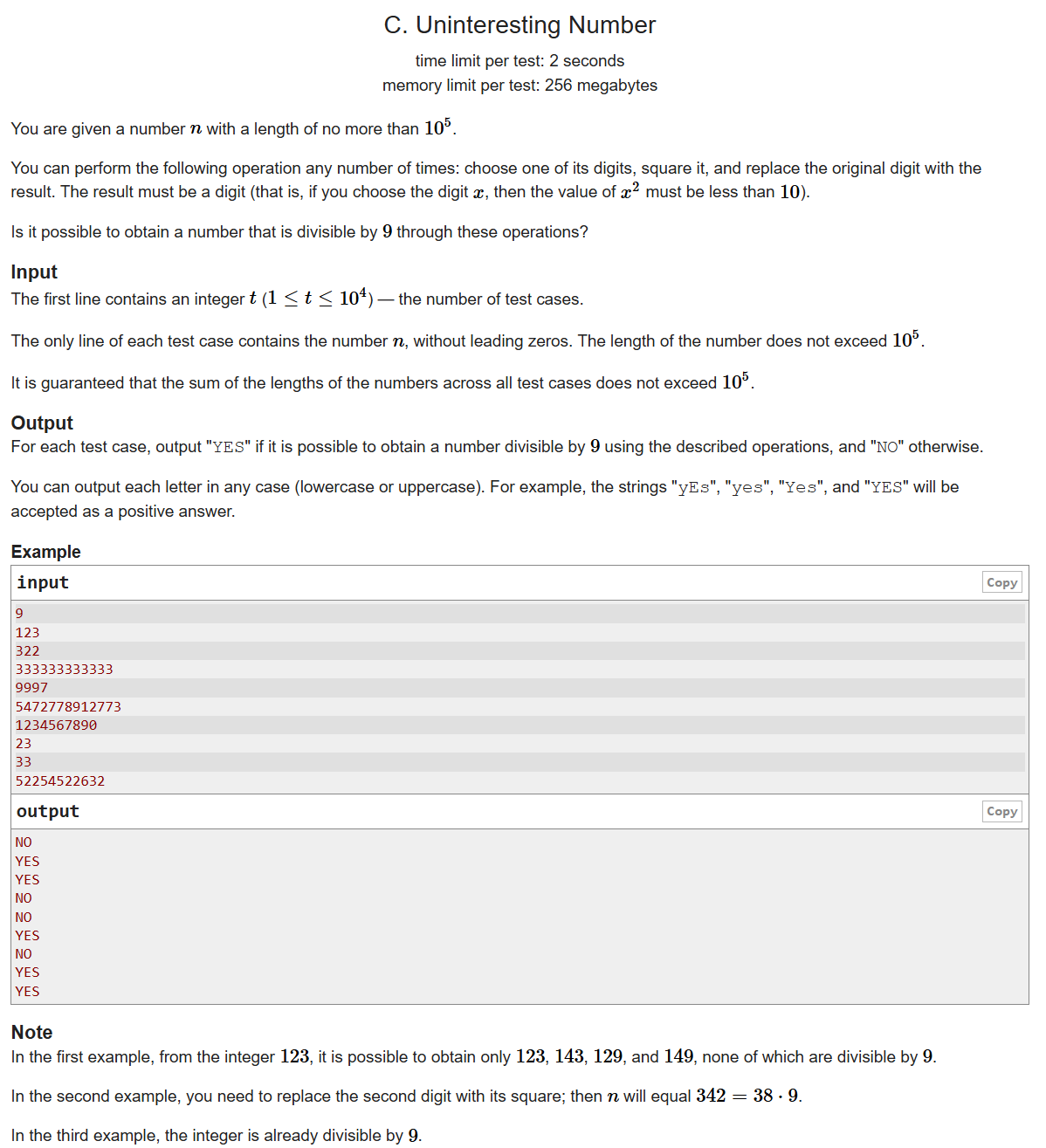
题目大意:给你一个位数不超过1e5的数,你可以把里面的任意个1,2,3进行平方处理,问你是否可以出 现处理之后的数能被9整除?
数的位数可以长达1e5,就需要用字符串来处理;小学老师讲过,能被9整除的数,该数的每一位数字之和可以被9整除。所以用sum来记录每位数之和,er记录2出现的次数,san记录3出现的次数。如果sum不能被9整除,那么就跑暴力:判断sum+er_i2+san_i6是否能被9整除
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| #include <bits/stdc++.h>
using namespace std;
void add_er_san(int sum,int er,int san){
for(int i=0;i<=er;i++){
for(int j=0;j<=san;j++){
if((sum+i*2+j*6)%9==0){
cout << "YES\n";
return;
}
}
}
cout << "NO\n";
return;
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
string n;int sum=0,er=0,san=0;
cin >> n;
int len = n.size();
for(int i=0;i<len;i++){
int ni = n[i] - '0';
sum += ni;
if(ni == 2) er++;
else if(ni == 3) san++;
}
if(sum%9 == 0){
cout << "YES\n";
continue;
}
add_er_san(sum,er,san);
}
return 0;
}
|
D
题目
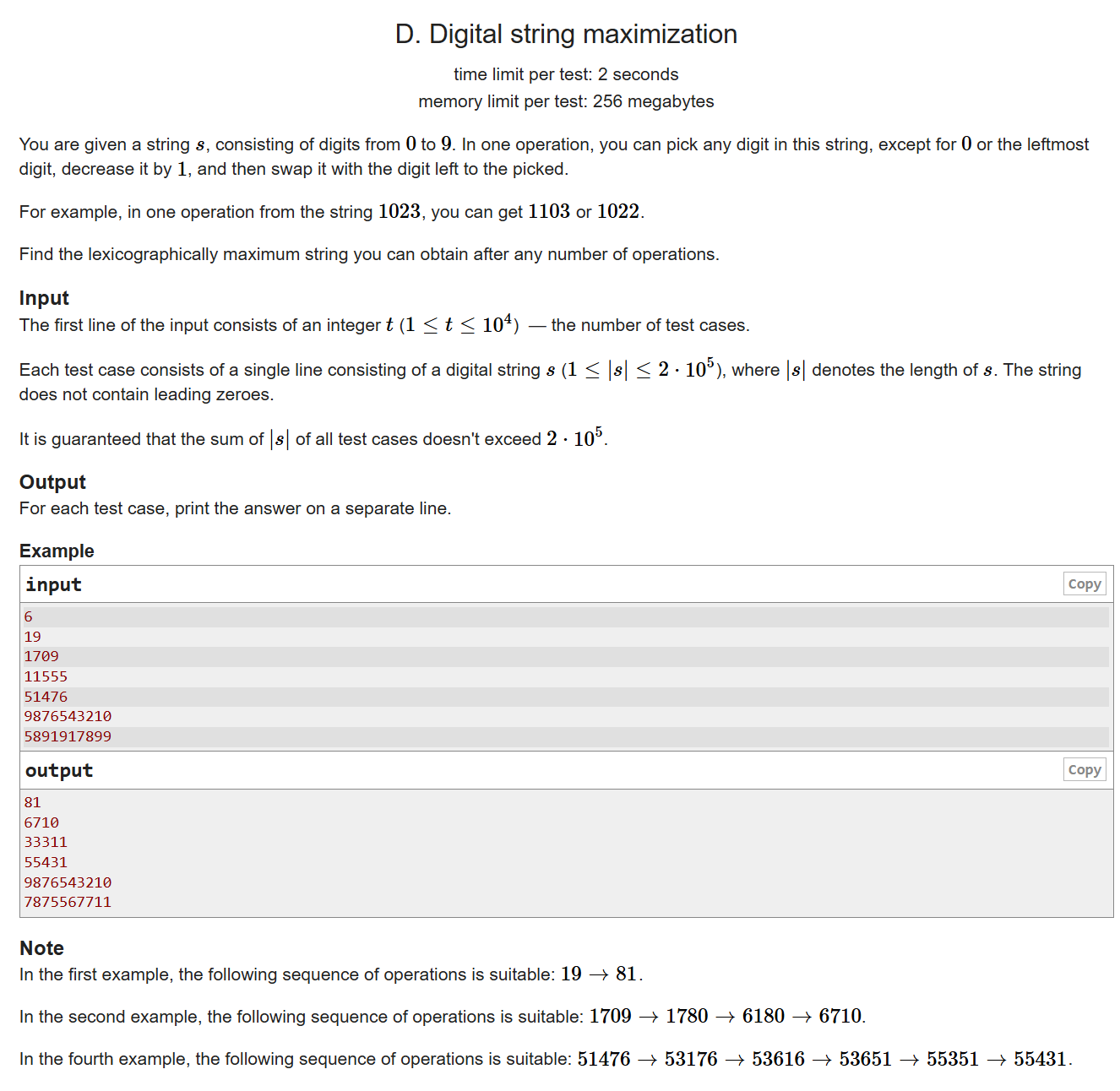
给你一个由0~9组成测字符串s,你可以把除了最左边的和0以外的数做这种操作:
该数-1,然后和它左边的数对调
问你任意次操作后能得到的词序最大的字符串是什么
显然,想让数尽可能大,就要尽可能让大的数排在左边。每一位数最大为9,最多移动9格,所以对于每一位数,考虑它右边9格之内的数,哪个数移到该格最大就移动哪个数
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
string n;
cin >> n;
int len = n.size();
if(len == 1){
cout << n[0] << '\n';
continue;
}
for(int i=0;i<len;i++){
int t = n[i]-'0',index=0;
for(int j=1;j<=9 && i+j<len;j++){
if(n[i+j]-'0'-j > t){
t=n[i+j]-'0'-j;
index=i+j;
}
}
if(index == i) continue;
for(int j=index;j>i;j--){
swap(n[j],n[j-1]);
}
n[i]=t+'0';
}
for(int i=0;i<len;i++)
cout << n[i];
cout << '\n';
}
return 0;
}
|
E
题目

题目大意:输入字符串a,b,字符串c由a,b融合来组成(ab融合时不能改变每个字符原本的前后顺序,如字符串a是er,字符串b是f,则字符串c不能为ref,可以为erf,efr,fer)
再输入一个可能被更改过的字符串c,问你a和b融合后至少要更改几个字符才能变成给出的字符串c
思路:dp,用dp[i][j]来表示c的前i+j个字符需要修改的字符数,a对应i,b对应j
一般状态转移方程为
dp[i][j] = min(dp[i-1][j] + (a[i-1]!=c[i+j-1]), dp[i][j-1] + (b[j-1]!=c[i+j-1]))
有i=0和j=0的特判,这俩表示只用b和只用a来组成c
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| #include <bits/stdc++.h>
using namespace std;
int dp[1001][1001];
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
string a,b,c;
for(int i=0;i<1001;i++)
for(int j=0;j<1001;j++)
dp[i][j]=0;
cin >> a >> b >> c;
int len_a=a.size(),len_b=b.size();
for(int i=0;i<=len_a;i++){
for(int j=0;j<=len_b;j++){
if(i==0 && j==0) continue;
else if(i==0) dp[i][j] = dp[i][j-1] + (b[j-1]!=c[j-1]);
else if(j==0) dp[i][j] = dp[i-1][j] + (a[i-1]!=c[i-1]);
else dp[i][j] = min(dp[i-1][j] + (a[i-1]!=c[i+j-1]), dp[i][j-1] + (b[j-1]!=c[i+j-1]));
}
}
cout << dp[len_a][len_b] << '\n';
}
return 0;
}
|
牛客月赛109
A
题目
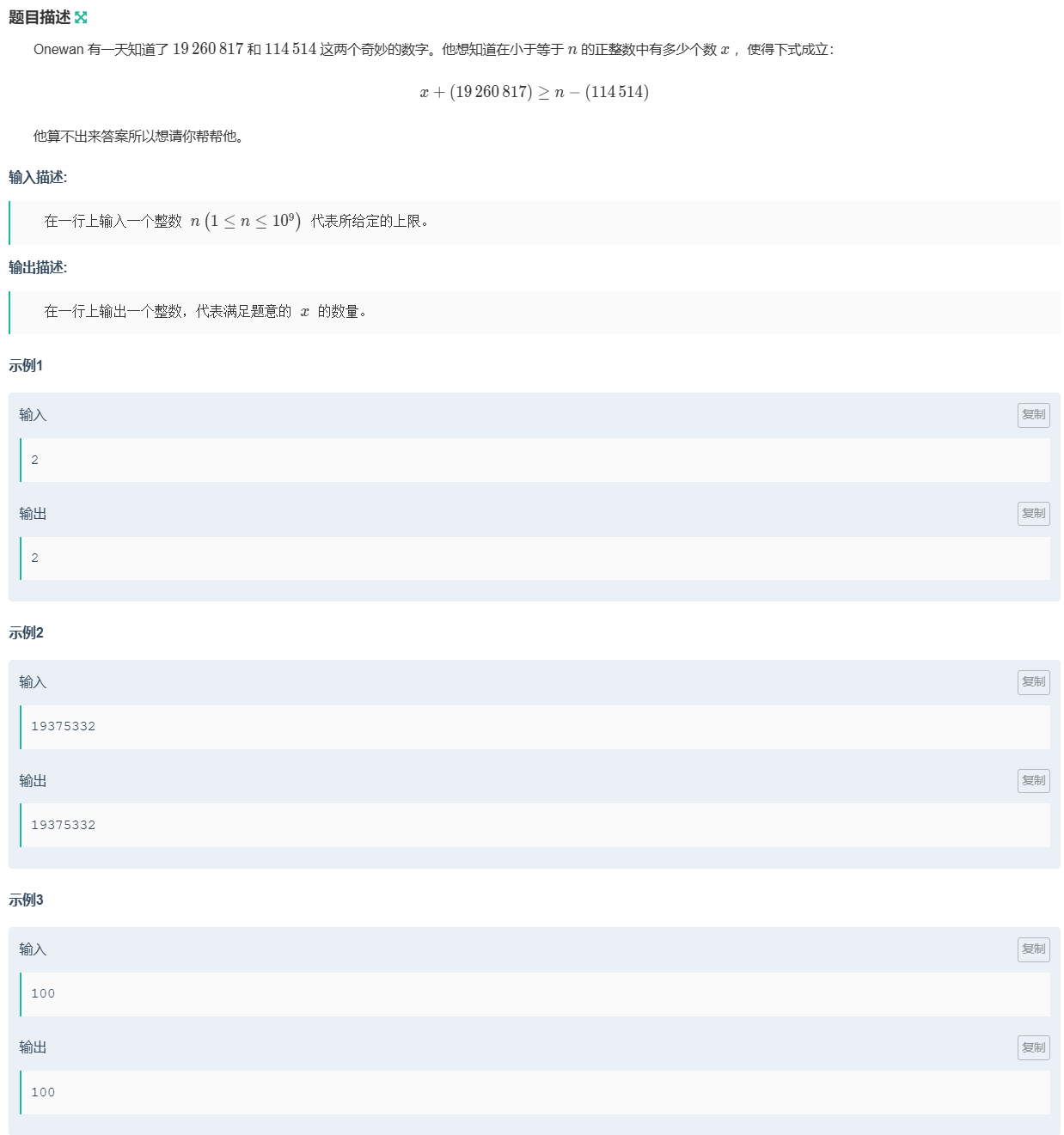
如题,这题可以不跑暴力,观察得到,如果n小于19375332,那么x=n;否则x=19375332
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
| #include <bits/stdc++.h>
#define int long long
using namespace std;
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n;
cin >> n;
if(n<=19375332) cout << n;
else cout << 19375332;
return 0;
}
|
B
题目
贪心
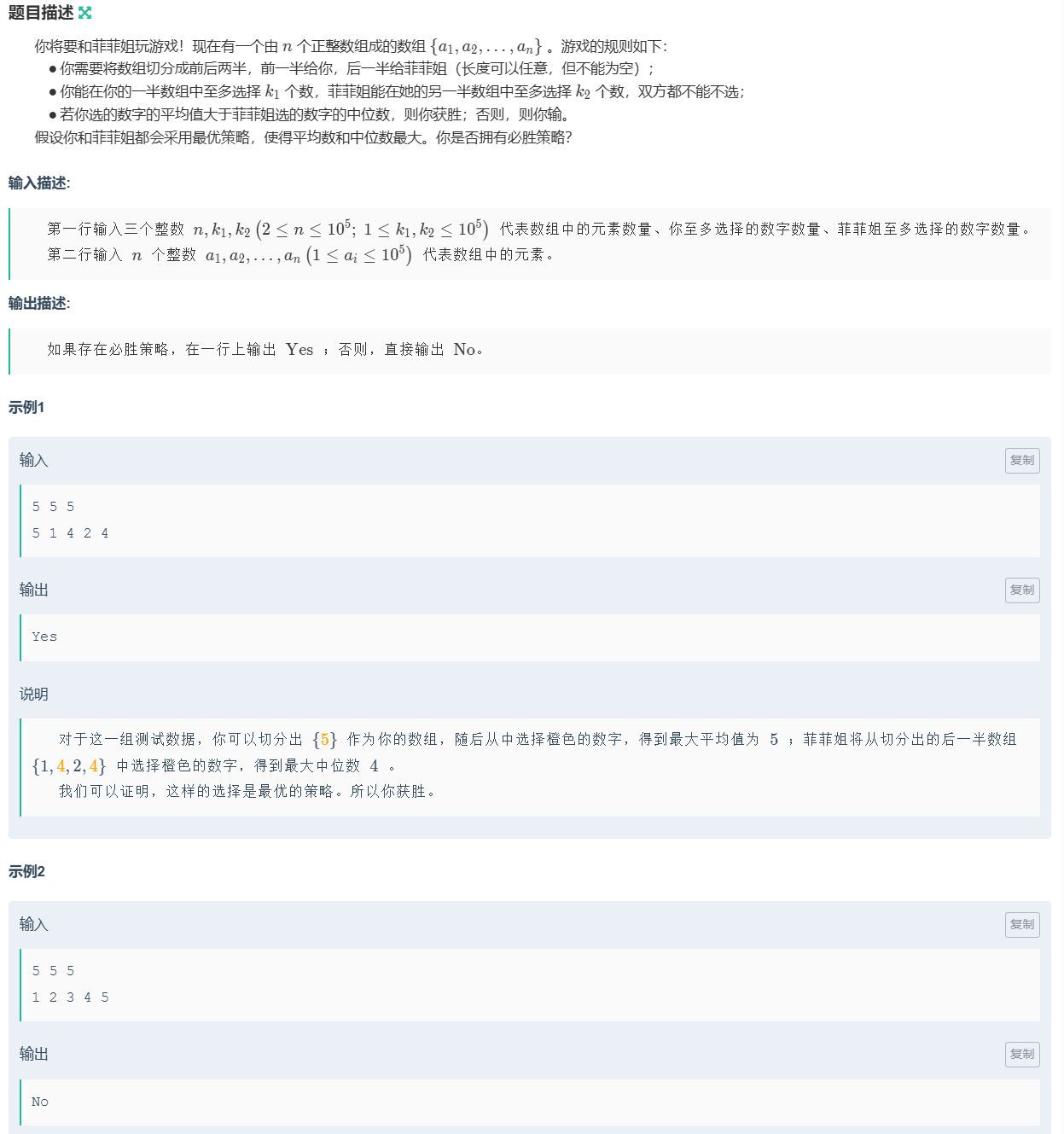
数组是自己切的,自己只能取数组的左边部分,右边部分给菲菲jj;想要使自己的平均数最大,那么可以只从自己的数组中取一个数——最大的那一个数,而欲使自己的数组中的最大的数尽可能大,就要让自己的数组中的数尽可能多,所以要把给的前n-1个数全部划分给自己,剩下的一个给菲菲jj;自己选出最大的平均数后,菲菲jj的唯一的数就是她的最大的中位数。最后判断就行
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| #include <bits/stdc++.h>
using namespace std;
vector <int> v1;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n,k1,k2,cache;
cin >> n >> k1 >> k2;
for(int i=0;i<n-1;i++){
cin >> cache;
v1.push_back(cache);
}
cin >> cache;
sort(v1.begin(),v1.end(),greater<int>());
if(v1[0]>cache) cout << "Yes\n";
else cout << "No\n";
return 0;
}
|
C
题目
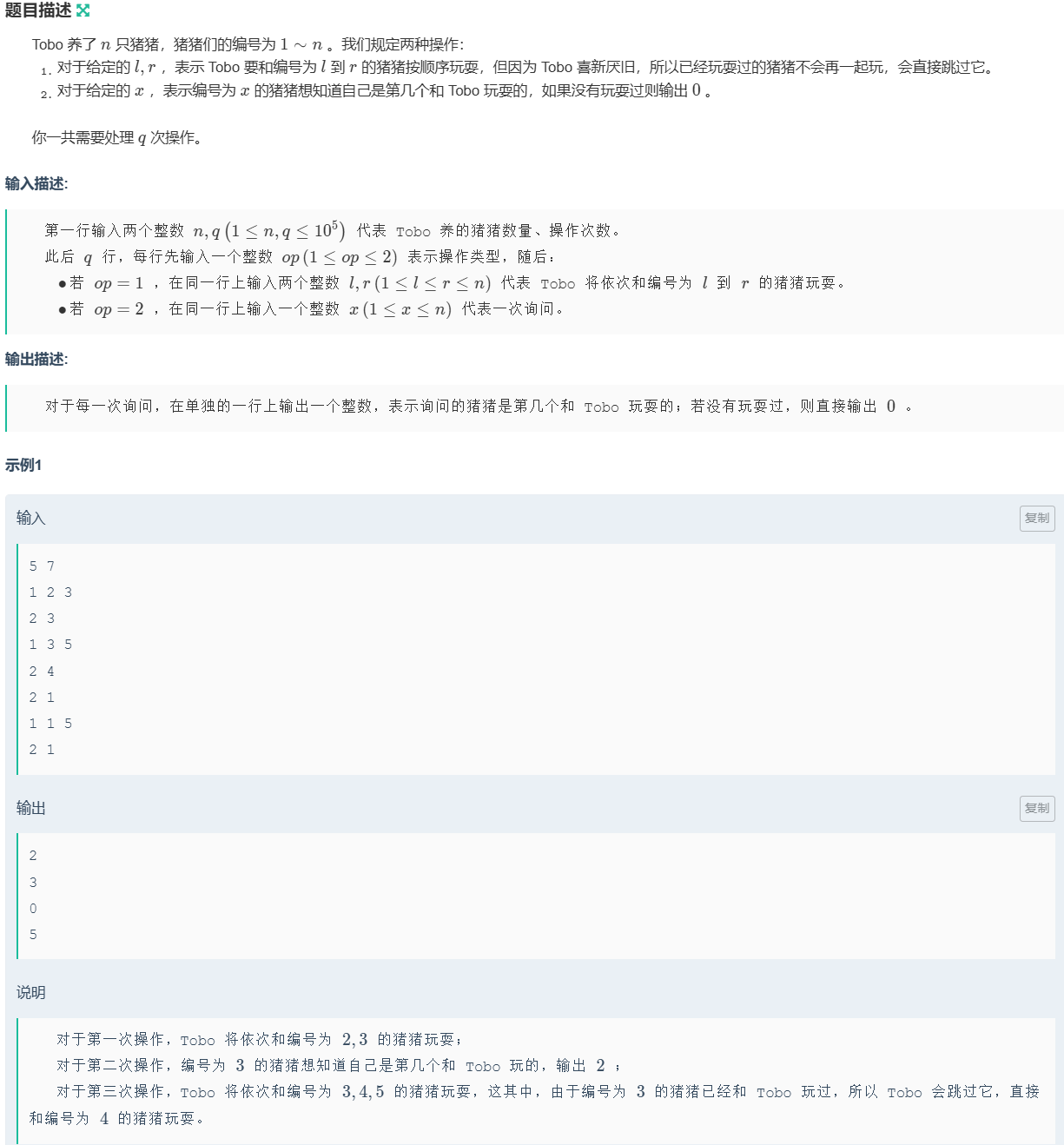
题目如图
这道题按常规思路去做必定TLE,l到r一个一个去遍历的这种枚举做法 在最坏的情况下会使时间复杂度来到O(n2) , 带入数据得出1e10,所以必定TLE
可以用一个数组来优化。这个数组储存每次的查询入口,如果这段区间的猪儿还没有被主人玩过,那么这段区间的入口都设为r+1,表示如果下次访问到了这段区间,就跳到r+1之后再做访问。时间复杂度可以优化到O(nlogn)
这个优化方法和并查集非常像,但是比并查集简单很多
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| #include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5;
int van[maxn+1],jump[maxn+1];
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n,q,op,l,r,x,index=0;
cin >> n >> q;
while(q--){
cin >> op;
if(op==1){
cin >> l >> r;
l--;r--;
while(l<=r){
if(!van[l]){
van[l] = ++index;
jump[l++] = r+1;
}
else l=jump[l];
}
}
else{
cin >> x;
cout << van[x-1] << '\n';
}
}
return 0;
}
|
D
题目

这道题我赛时没有做,下来学了背包后做的
用sum表示一个猪儿都不陪,全部用钱搞定
用s[i]表示第i只猪儿要从哪一天开始陪
用day[i]表示调整值
day[s[i]+m-1]=min(day[s[i]+m-1],bi-vali)
用dp[i]表示到第i天的最小费用,状态转移方程为:
dp[i]=min(dp[i-1],dp[i-m]+day[i])
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| #include <bits/stdc++.h>
#define int long long
using namespace std;
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n,m,sum=0;
cin >> n >> m;
vector <int> s(n+1),day(n+1,1e18),dp(n+1);
for(int i=1;i<=n;i++) cin >> s[i];
for(int i=1;i<=n;i++){
int bi,vali;
cin >> bi >> vali;
sum+=vali;
day[s[i]+m-1] = min(day[s[i]+m-1],bi-vali);
}
for(int i=m;i<=n;i++)
dp[i] = min(dp[i-1],dp[i-m]+day[i]);
cout << sum+dp[n] << '\n';
return 0;
}
|
牛客周赛77
A
题目
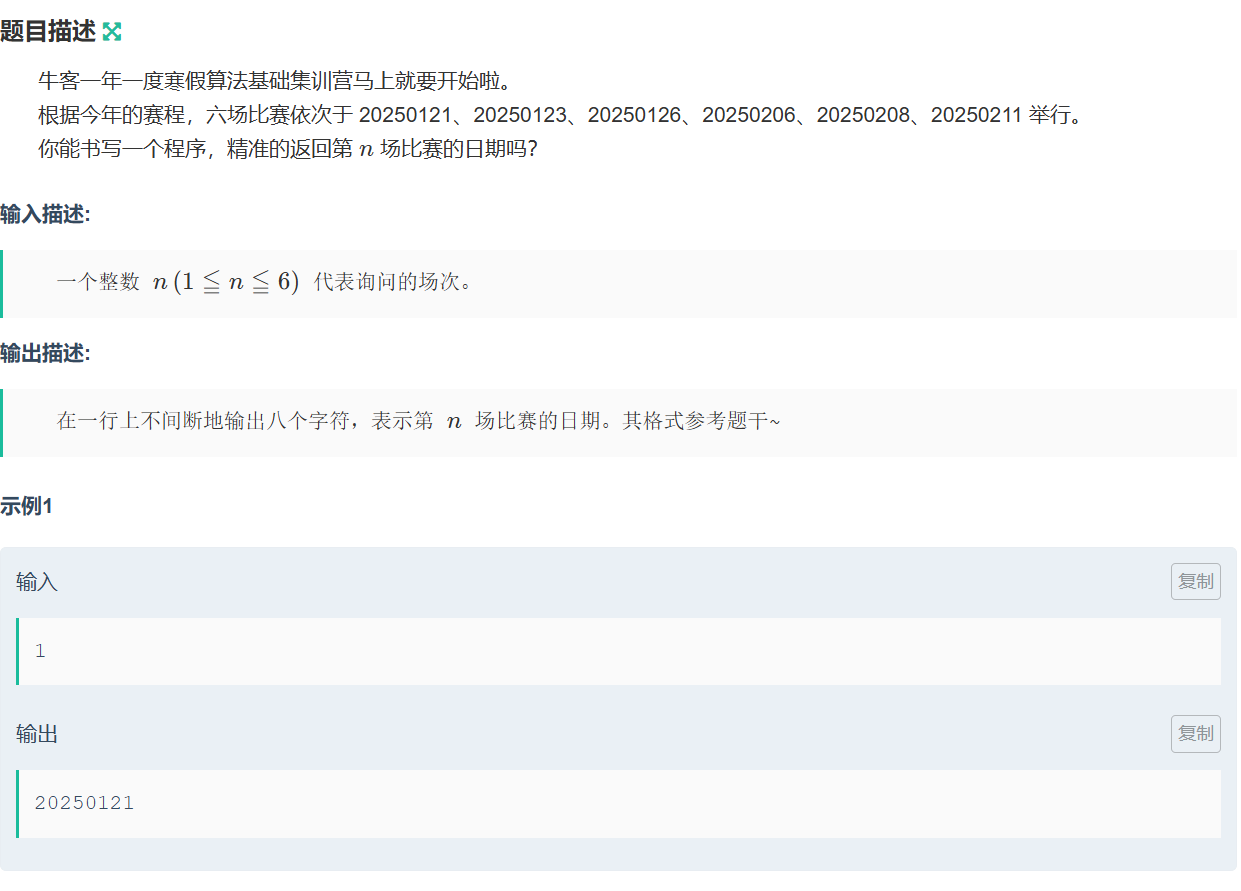
纯签到
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| #include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
if(t==1) cout << 20250121;
else if(t==2) cout << 20250123;
else if(t==3) cout << 20250126;
else if(t==4) cout << 20250206;
else if(t==5) cout << 20250208;
else cout << 20250211;
return 0;
}
|
B
题目
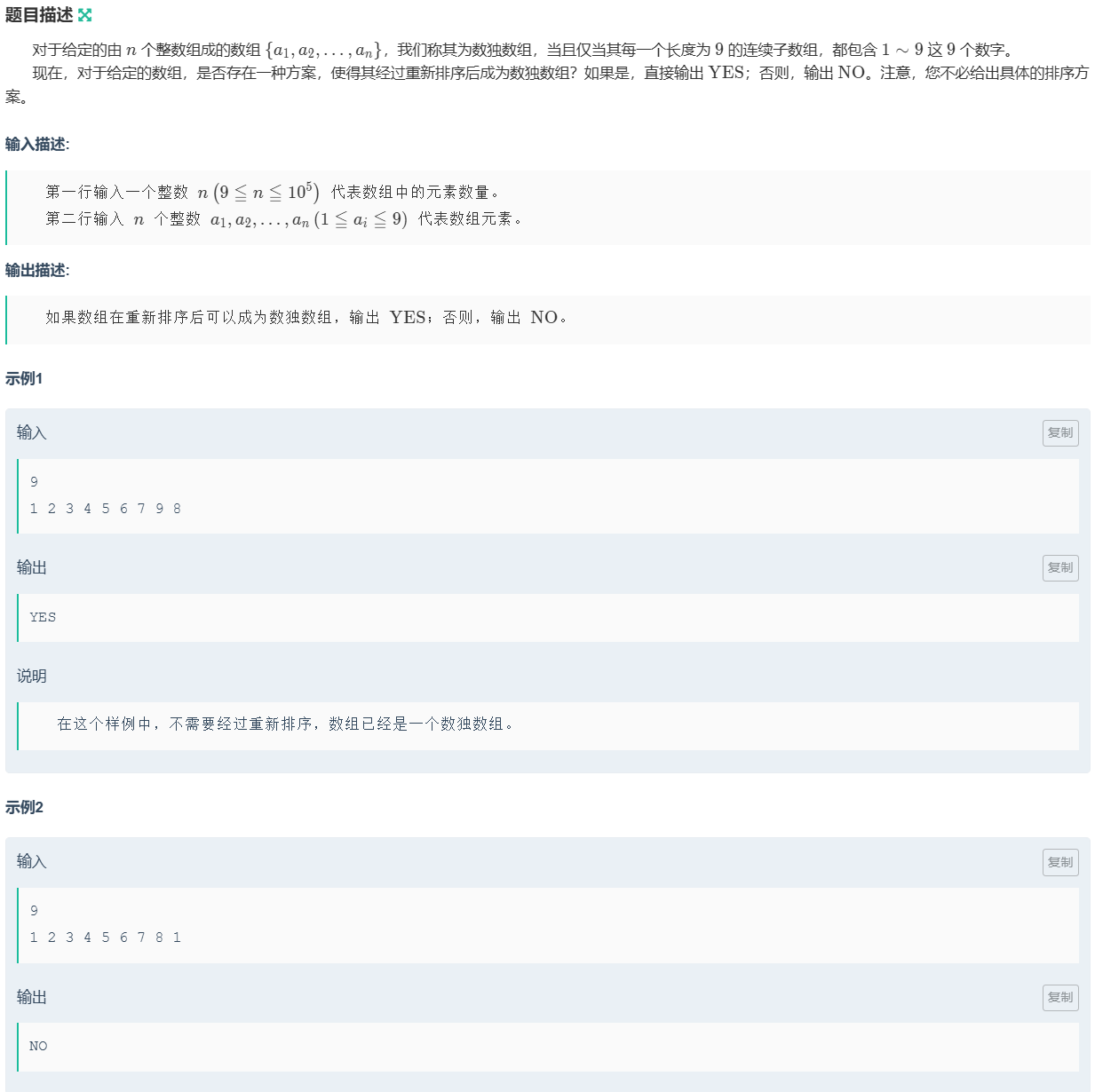
题目如图
这道题很像一层一层铺砖块,把这层铺完了才开始铺下一层
那么没有所有没有铺完的砖块层的层数差不会超过1
如果超过1了,就不行
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| #include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int a[10]={0},t,cache;
cin >> t;
for(int i=0;i<t;i++){
cin >> cache;
a[cache]++;
}
int pd=0,maxn=-1,minn=99999999;
for(int i=1;i<10;i++){
maxn=max(maxn,a[i]);
minn=min(minn,a[i]);
}
if(maxn-minn>1) pd=1;
cout << (pd==0 ? "YES\n":"NO\n");
return 0;
}
|
C
题目
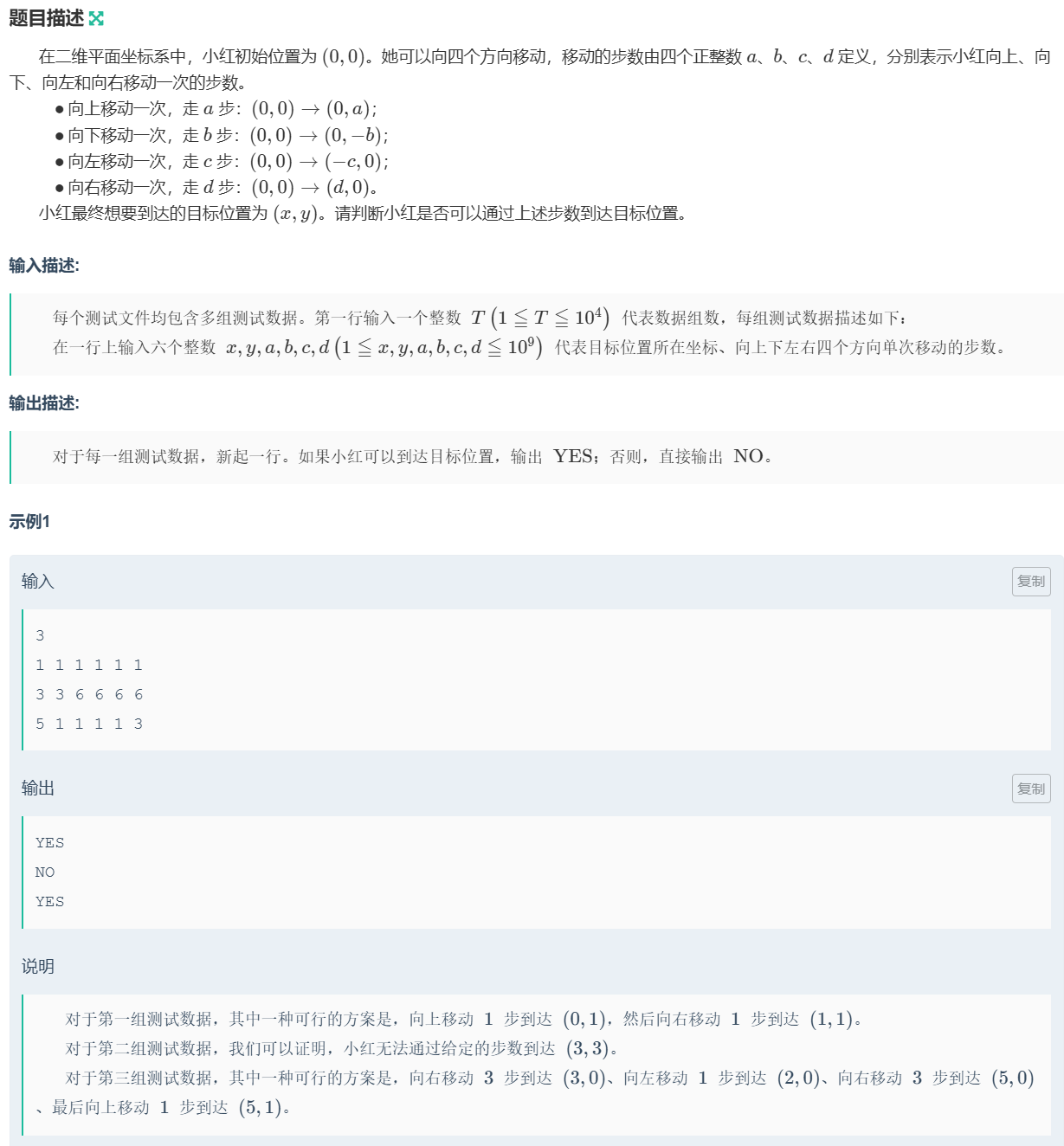
如题,实质上是最大公约数的运用
对终点坐标x和y分开判断,x(或y)如果是cd(或ab)的最大公约数的倍数,那么就能走到
否则走不到
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| #include <bits/stdc++.h>
#define int long long
using namespace std;
int gcd(int a,int b){
return (b==0 ? a : gcd(b,a%b));
}
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int x,y,a,b,c,d;
cin >> x >> y >> a >> b >> c >> d;
if(x%gcd(c,d)==0 && y%gcd(a,b)==0) cout << "YES\n";
else cout << "NO\n";
}
return 0;
}
|
codeforces 998 div.3
A
题目

定义斐波那契数:ai+2=ai+ai+1
给你一个串数,你要在a1、a2、a4、a5四个数的中间插入a3,a3可以是任意整数
问你这串数中有多少个斐波那契数
思路:令给的数是a b c d,让x1=a+b,x2=c-b,x3=d-c
只需要判断:如果x1、x2、x3都相等,那么斐波那契数有3个;如果其中有两个相等,那么斐波那契有2个,否则1个
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| #include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int a,b,c,d,x1,x2,x3;
cin >> a >> b >> c >> d;
x1=a+b,x2=c-b,x3=d-c;
if(x1==x2 && x2==x3)
cout << "3\n";
else if((x1==x2 && x1!=x3) || (x1==x3 && x1!=x2) || (x2==x3 && x1!=x2))
cout << "2\n";
else cout << "1\n";
}
return 0;
}
|
B
题目
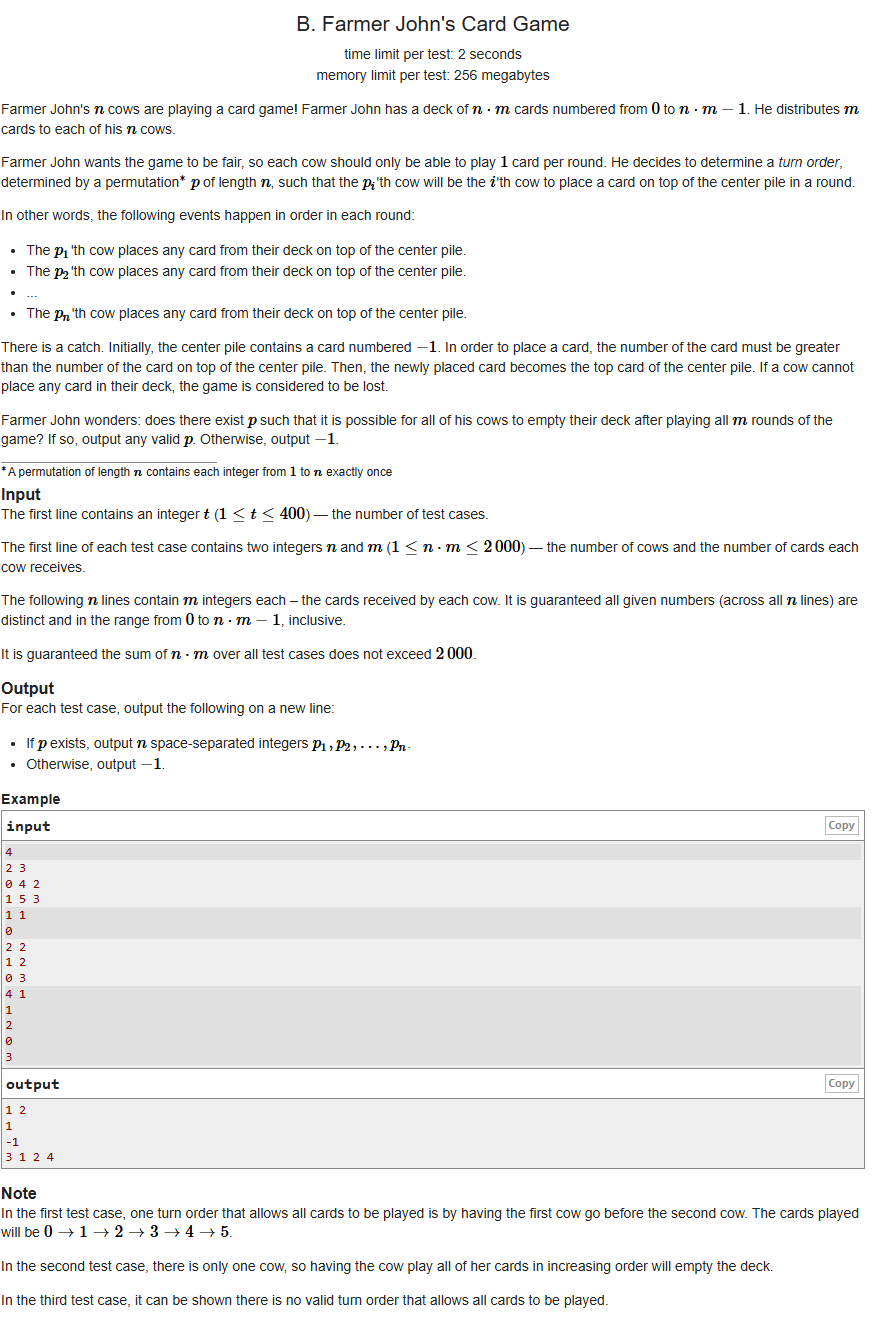
n头牛儿打牌,每个牛儿有m张牌,每个回合这n个牛儿都按顺序轮流出牌,要求第n头牛出的牌要比第n-1头出的大。
问你是否存在一种出牌顺序
思路:先用一个数组a记录从1到n*m对应的牛儿;由于每回合每个牛儿出牌顺序是固定的,我们用数组b记录第一回合的出牌顺序,也就是a的前n个。然后模拟每回合,判断b[i]是否等于a[i+j],只要出现不等于的情况就不行
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int a[2001]={0},b[2001]={0},n,m,cache;
cin >> n >> m;
for(int i=1;i<=n;i++){
for(int j=0;j<m;j++){
cin >> cache;
a[cache]=i;
}
}
for(int i=0;i<n;i++) b[i]=a[i];
int nm=n*m,pd=1;
for(int i=0;i+n<=nm && pd;i+=n)
for(int j=0;j<n;j++)
if(b[j]!=a[i+j]){
pd=0;
break;
}
if(!pd) cout << -1;
else for(int i=0;i<n;i++) cout << b[i] << ' ';
cout << '\n';
}
return 0;
}
|
C
题目

给出n(偶数)个数,k,游戏进行n/2轮
每一轮依次进行以下操作:
Alice选择一个数a并从列表里删除它
Bob选择一个数b并从列表里删除它
如果a+b=k,分数+1
Alice的目标是使分数尽可能小,而Bob的目标是使分数尽可能大。假设双方都采用最优策略,问你游戏结束后分数是多少
思路:先把k拆成1+(k-1),2+(k-2)…这种成对的形式,然后判断列表里有多少个完整的对,这个成对的数目就是原始分数
Alice肯定会优先从大于等于k的数里面选择,因为没有另外一个正整数使得它们之和等于k,Alice选了大于等于k的数之后如果还有这种数,Bob也要选;如果没有大于等于k的数了,Bob就要从小于K的没有结成对的数里选;如果没有没有结成对的数,那么就让原始分数-1,意味着拆开一对数,拿其中一个去和Alice抵消
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include <bits/stdc++.h>
using namespace std;
const int maxn = 4e5;
int a[maxn+1];
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n,k,cache,score=0,res=0,alice=0;
memset(a,0,maxn+1);
cin >> n >> k;
for(int i=0;i<n;i++){
cin >> cache;
if(cache >= k) alice++;
else a[cache]++;
}
for(int i=1;i<=k/2;i++){
int j=k-i;
if(i==j){
score += a[i]/2;
res += a[i]%2;
}else{
score += min(a[i],a[j]);
res += abs(a[i]-a[j]);
}
}
if(res >= alice%2) cout << score << '\n';
else{
cout << score-1<< '\n';
}
}
return 0;
}
|
D
题目

给出一串数,你可以做任意次以下操作:
从第1个到第n-1个数中选一个数ai,ai和ai+1都要减去min(ai,ai+1)
问你能否出现一个不递减的数列
思路:思考后发现,从1到n-1依次做这种操作,如果出现了ai不等于0,而ai+1等于0,那么就不行,否则可以。从局部到整体,贪心
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| #include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5;
int a[maxn+1];
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n,pd=1;
memset(a,0,maxn+1);
cin >> n;
for(int i=0;i<n;i++)
cin >> a[i];
for(int i=0;i<n-1;i++){
int minn = min(a[i],a[i+1]);
a[i]-=minn,a[i+1]-=minn;
if(a[i+1]==0 && a[i]!=0){
pd=0;
break;
}
}
cout << (pd ? "YES\n":"NO\n");
}
return 0;
}
|
Algorithm–算法学习
倍增法
倍增就是"成倍增长",利用二进制本身倍增的特性,第i位的权值2i等于前面所有权值的和,即
2i** = 2**i-1** + 2**i-2** + … + 2**1+20** +1**
一个整数n,它的二进制只有log2n位。如果要从0增长到n,可以以1,2,4,…,2k为跳板快速跳到n,这些跳板只有k=log2n个
书上举了洛谷的一道题为例:P4155 国旗计划

主要用到化圆为线,贪心求最优区间,倍增优化
化圆为线,把原来的圆圈复制再相接以保持首尾关系
贪心,每个区间的左端点排序,在区间x后面的区间里选择不超过x区间右端点的最大左端点的区间
倍增,go[s][i]表示从第s个区间出发,走2i个最优区间后到达的区间
关键递推式: go[s][i] = go[go[s][i-1]][i-1]
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| #include <bits/stdc++.h>
using namespace std;
const int N = 4e5+1;
int n,m,n2;
int go[N][20];
struct soldier{
int id,l,r;
bool operator < (const soldier b) const{return l<b.l;}
}s[N*2];
void init(){
int nxt=1;
for(int i=1;i<=n2;i++){
while(nxt<n2 && s[nxt].l<=s[i].r)
nxt++;
go[i][0] = nxt-1;
}
for(int i=1;(1<<i)<=n;i++)
for(int j=1;j<=n2;j++)
go[j][i] = go[go[j][i-1]][i-1];
}
int res[N];
void answer(int x){
int len=s[x].l+m,cur=x,ans=1;
for(int i=log2(N);i>=0;i--){
int pos = go[cur][i];
if(pos && s[pos].r<len){
ans+=1<<i;
cur=pos;
}
}
res[s[x].id] = ans+1;
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin >> n >> m;
for(int i=1;i<=n;i++){
s[i].id=i;
cin >> s[i].l >> s[i].r;
if(s[i].r<s[i].l) s[i].r+=m;
}
sort(s+1,s+n+1);
n2=n;
for(int i=1;i<=n;i++){
n2++;
s[n2] = s[i];
s[n2].l = s[i].l+m;
s[n2].r = s[i].r+m;
}
init();
for(int i=1;i<=n;i++) answer(i);
for(int i=1;i<=n;i++) cout << res[i] << ' ';
return 0;
}
|
01背包
(这只是正式开始学习背包,但是由于做题的原因,之前已经接触了一些背包问题、零零散散地学了一些了)
01背包问题通常为:给定n种物品和一个背包,第i个物品体积为ci,价值为wi,背包地容量为C。如何选择装入背包的物品,使装入背包中的物品的总价值最大?
以 HDU 2602 为例
题目
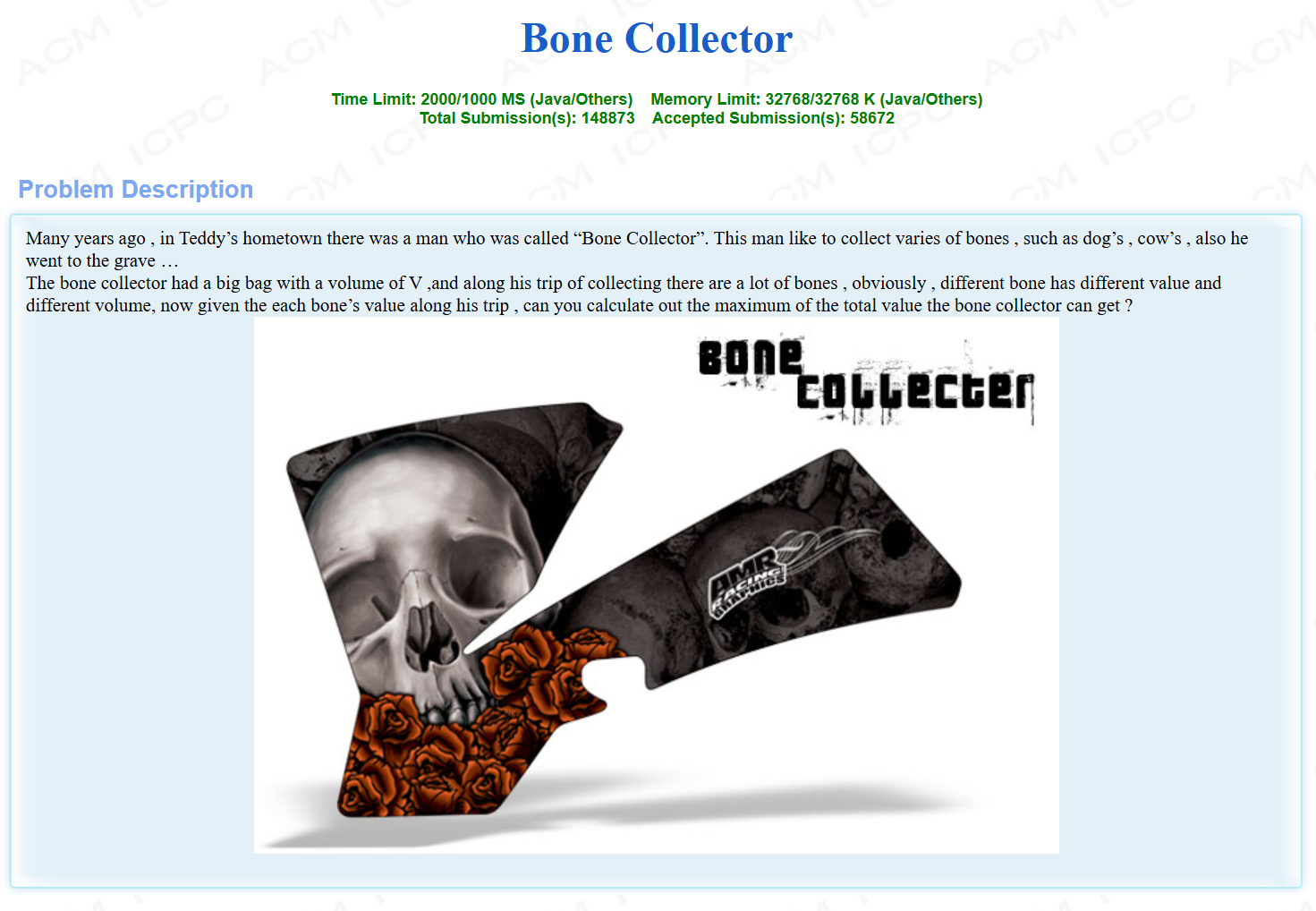
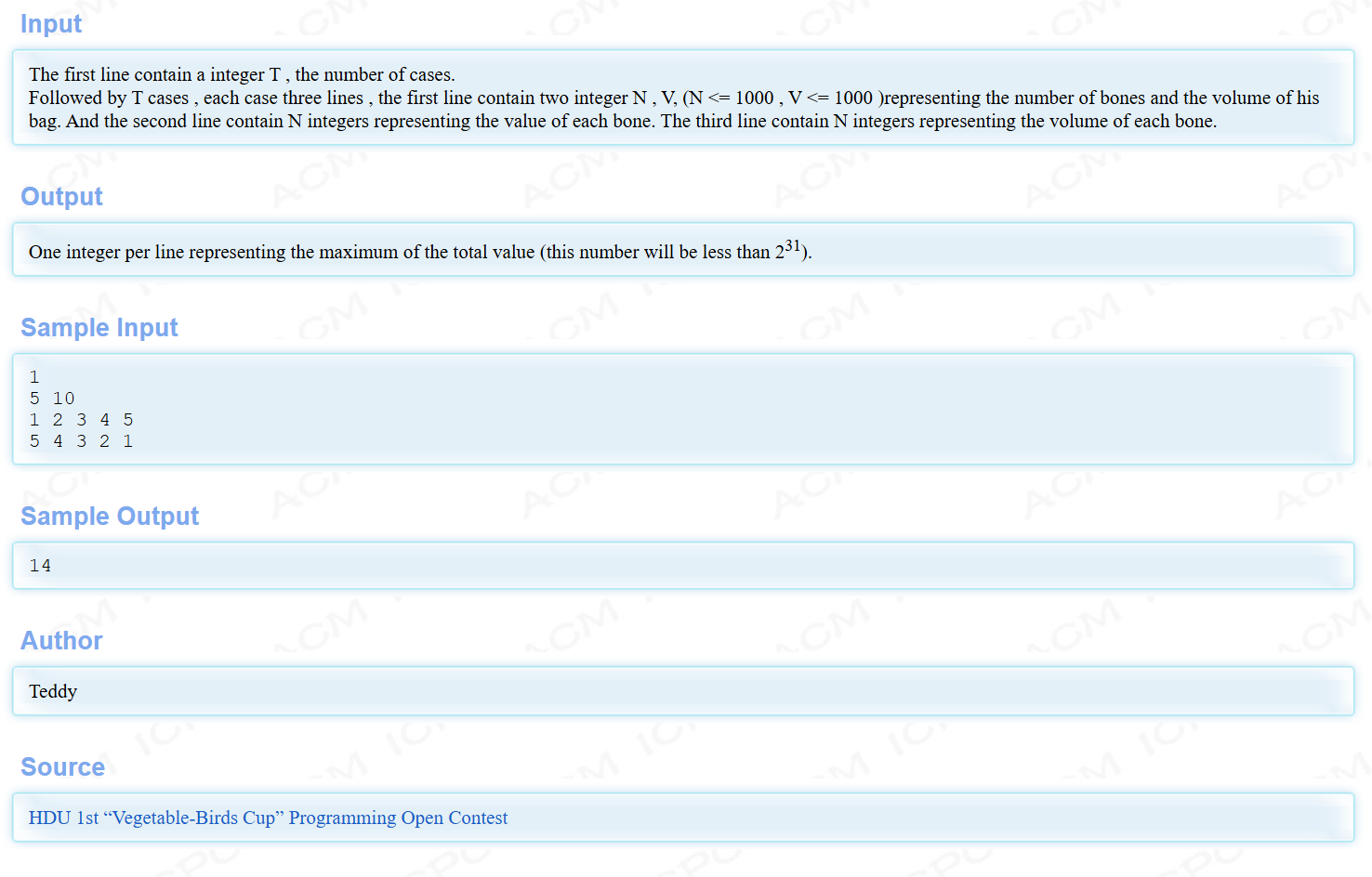
用自底向上的递推完成转移过程,dp[i][j]表示把前i个物品(从第1个到第i个)装入容量为j的背包中获得的最大价值。假设现在递推到dp[i][j],分两种情况:
(1) 第i个物品的体积比j还大,则不能装入当前背包,直接继承前i-1个物品装入容量为j的背包,即dp[i][j] = dp[i-1][j]
(2) 第i个物品体积比j小,能装进背包,又分为两种:装或不装
① 装。 dp[i][j] = dp[i-1][j-c[i]] + w[i]
② 不装。 dp[i][j] = dp[i-1][j]
取①②中的最大值,状态转移方程为
dp[i][j] = max(dp[i-1][j-c[i]]+w[i],dp[i-1][j])
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include <bits/stdc++.h>
using namespace std;
const int N = 1001;
int w[N],c[N],dp[N][N];
int solve(int n,int C){
for(int i=1;i<=n;i++)
for(int j=0;j<=C;j++){
if(c[i] > j) dp[i][j] = dp[i-1][j];
else dp[i][j] = max(dp[i-1][j],dp[i-1][j-c[i]]+w[i]);
}
return dp[n][C];
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n,C;
cin >> n >> C;
for(int i=1;i<=n;i++)
cin >> w[i];
for(int i=1;i<=n;i++)
cin >> c[i];
memset(dp,0,sizeof(dp));
cout << solve(n,C) << '\n';
}
return 0;
}
|

























