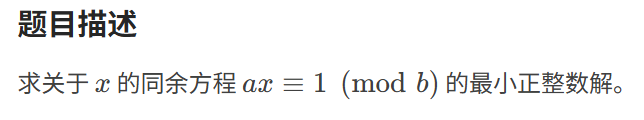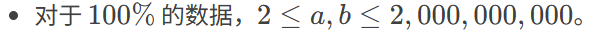欧几里得算法(辗转相除法) 求最大公约数
C++的库有 __gcd()函数,赛时推荐直接用这个。博文里讲讲原理和实现
原理是:两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数
gcd(a,b)=gcd(b,a%b)
用递归来实现
1
2
3
| int gcd(int a,int b){
return b==0 ? a : gcd(b,a%b);
}
|
最小公倍数
先求最大公约数gcd(a,b)
1
2
3
| int gcd(int a,int b){
return b==0 ? a : gcd(b,a%b);
}
|
最小公倍数 lcm(a,b) 与其的关系为:
gcd(a,b)∗lcm(a,b)=a∗b
因此
lcm(a,b)=(a∗b)/gcd(a,b)
1
2
3
| int lcm(int a,int b){
return a/gcd(a,b)*b;
}
|
素数筛
试除法
设n=a×b,有min(a,b)≤n,令a≤b,只要检查[2,n]内的数,如果n不是素数,就能找到一个 a。试除法的复杂度是O(n),对于n≤1012的数是没有问题的。
1
2
3
4
5
6
| bool is_prime(int n){
if(n<=1) return false;
for(int i=2;i*i<=n;i++)
if(n%i==0) return false;
return true;
}
|
埃拉托斯特尼筛法(埃氏筛)
从2开始,不断筛掉2的倍数,3的倍数,5的倍数,7的倍数,11的倍数…
埃氏筛简单易用,其时间复杂度为O(nloglog2n),近似于O(n);其空间复杂度:当MAXN=1e7时约为10MB
1
2
3
4
5
6
7
8
9
10
11
12
13
| const int MAXN = 1e7+5;
vector <int> prime;
bool Visit[MAXN];
void sushu(int n){
for(int i=2;i*i<=n;i++){
if(!Visit[i])
for(int j=i*i;j<=n;j+=i)
Visit[j]=true;
}
for(int i=2;i<=n;i++)
if(!Visit[i])
prime.push_back(i);
}
|
欧拉筛(Sieve of Euler)
欧拉筛是一种线性筛,时间复杂度为 O(n) ,求得 1 n 内所有素数。欧拉筛是对埃氏筛的改进,可以避免对很多数的重复判定。
欧拉筛原理:
一个合数肯定有一个最小质因数;让每个合数只被它的最小质因数筛选一次,以达到不重复筛的目的。
欧拉筛可以处理约 n=1e8 的问题,bool vis[N]约100MB,因为N=1e8时有5761455个素数,因此int prime[5800000],约23MB,否则大小为N就会超出限制
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| const int N = 1e8;
int prime[5800000]={0};
bool vis[N]={0};
int euler_sieve(int n){
int cnt = 0;
for(int i=2;i<=n;i++){
if(!vis[i]) prime[cnt++] = i;
for(int j=0;j<cnt;j++){
if(i*prime[j] > n) break;
vis[i*prime[j]] = 1;
if(i%prime[j] == 0) break;
}
}
return cnt;
}
|
线性丢番图方程
方程ax+by=c称为二元线性丢番图方程,其中a、b、c为已知数,x、y为未知量,问是否有整数解。
ax+by=c实际上是二维x-y平面内的一条直线,这条直线上如果有整数点,那么方程就有解,且有无穷多个整数点(解);这条直线上没有整数点,那么方程就没有整数解。
ax+by=c有解的充分必要条件是d=gcd(a,b)能整数c
因为:
设a=d⋅a′,b=d⋅b′,其中gcd(a′,b′)=1
那么方程等价于
d(a′x+b′y)=c
因此c必须是d的整数倍才有解
如果(x0,y0)是一个特解,那么所有解(通解)可以表示为
{x=x0+db⋅ny=y0−da⋅n其中 n∈Z
因为:
(x0,y0)是一个格点(整数解的点),移动到另一个格点
(x0+Δx,y0+Δy),
有aΔx+bΔy=0,最小的整数解为Δx=b/d,Δy=−a/d
扩展欧几里得算法 与 二元丢番图方程的解
求解方程ax+by=c的关键是找到一个特解(x0,y0),
用扩展欧几里得算法求一个特解(x0,y0)的代码如下:
1
2
3
4
5
6
7
8
|
typedef long long ll;
ll extend_gcd(ll a,ll b,ll &x,ll &y){
if(b == 0){x = 1; y = 0; return a;}
ll d = extend_gcd(b,a%b,y,x);
y -= a/b * x;
return d;
}
|
该算法很高效,为(Olog min(a,b))
例题–洛谷P1516青蛙的约会
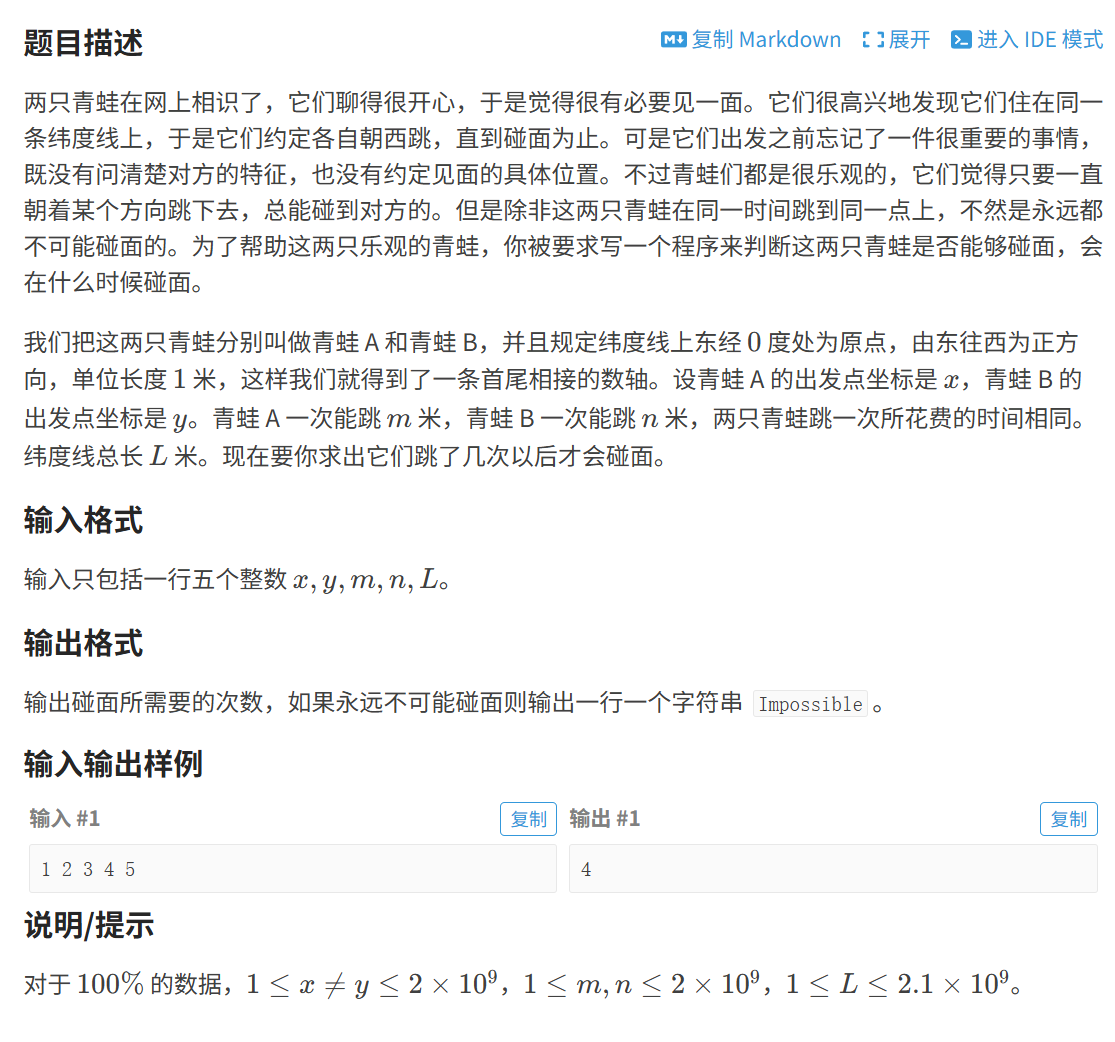
可以发现,两只青蛙跳的路程取余L是同余的,也就是方程
x+km≡y+kn (mod L)
k即为所求。变化方程为
x+km−(y+kn)=Lz , z∈Z
再将其变化为
k(m−n)−tL=−(x+y)
令W=(n−m),S=(x−y)
方程就变化为
kW+tL=S
这就是一个二元方程了,要做的就是求出最小解kmin
用exgcd解,方程就转化成
kjW+tjL=(W,L)
求出的kj就是一个特解
所有解可以表示为
ki=kj+cgcd(W,L)L
这个方程对于c∈Z而言,想通过特解推出一个最小解,可以这样做
kmin=kj mod gcd(W,L)L
而因为这个 k 是建立在 exgcd 得出的方程上的,方程右边是gcd(W,L)而不是S。所以最后我们需要将结果×gcd(W,L)S
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| #include <bits/stdc++.h>
using namespace std;
using ll = long long;
ll exgcd(ll a,ll b,ll &x,ll &y){
if(b == 0) {x = 1; y = 0; return a;}
int d = exgcd(b,a%b,y,x);
y -= a/b *x;
return d;
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
ll x,y,m,n,l;
cin >> x >> y >> m >> n >> l;
ll k,t, b = n-m, a = x-y;
if(b < 0){
b = -b;
a = -a;
}
int d = exgcd(abs(m-n),l,k,t);
if(a % d !=0) cout << "Impossible\n";
else cout << (k*a/d % (l/d) + (l/d))%(l/d) << '\n';
return 0;
}
|
裴蜀定理(贝祖定理)
如果a与b均为整数,则有整数x和y使得ax+by=gcd(a,b)
推论
整数a与b互素当且仅当存在整数x和y,使得ax+by=1
一道例题–洛谷P4549
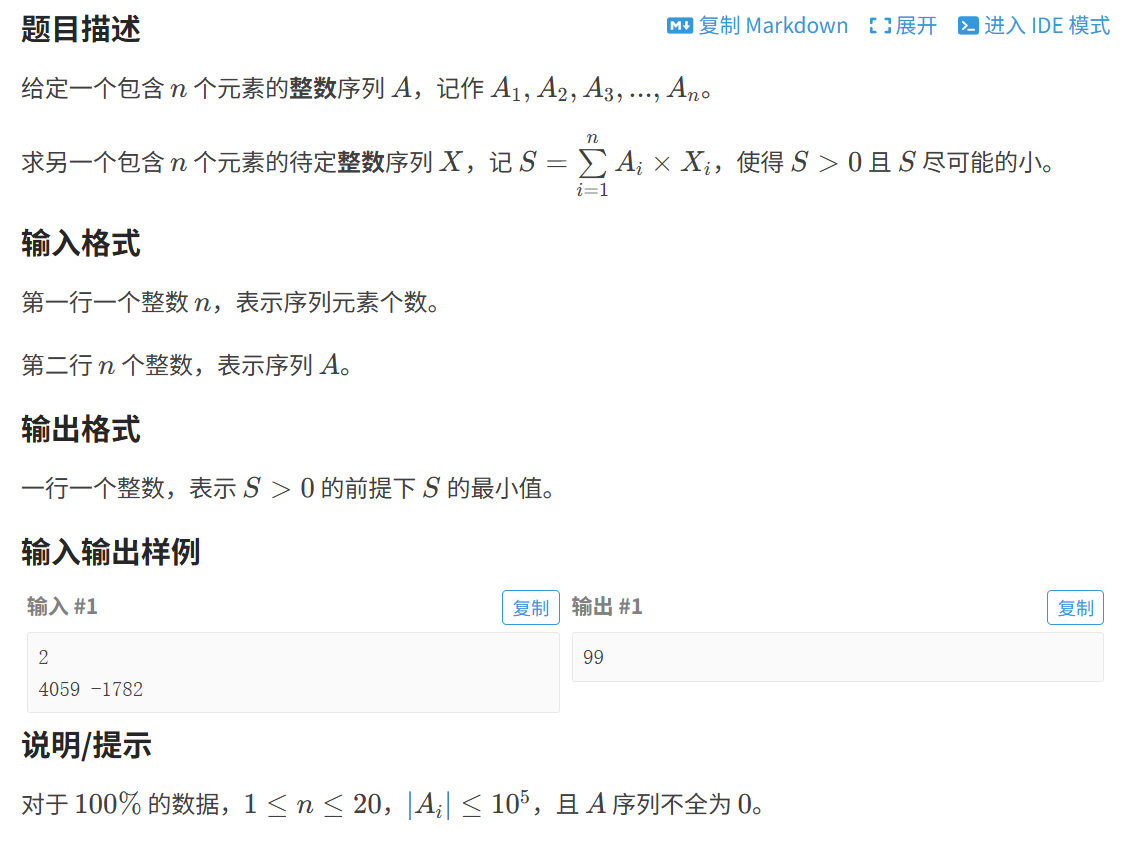
n = 1时,答案就是输入的数
n > 1时,先看前两个数A1X1+A2X2=C,由于d=gcd(A1,A2) ∣ C,显然这里S取gcd(A1,A2)时最小;后面的数和前面的结果进行gcd即可
注意,当Ai<0时,gcd可能会返回负数,因此最后一步输出正数即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| #include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n,num1;
cin >> n >> num1;
for(int i=2;i<=n;i++){
int num2;
cin >> num2;
num1 = __gcd(num1,num2);
}
cout << (num1>0 ? num1:-num1) << '\n';
return 0;
}
|
pick定理
在一个平面直角坐标系内,如果一个多边形的顶点都是格点,多边形的面积等于边界上格点数的一半加上内部的格点数减1,即s=2j+k−1
同余
a≡b (mod m)称为a和b模m同余
这里有m ∣ (a−b)
同余式转等式
若a和b是整数,m是正整数,则a≡b (mod m)当且仅当存在整数k,使得a=b+km。
例如19≡−2(mod 7),有19=−2+3×7
模运算性质
(a+b) % p=(a % p+b % p) % p(a×b) % p=(a % p×b % p) % p
这是加法和乘法的模运算。对于除法,也能满足
(a/b) % p=(a % p÷b % p) % p
吗
不满足!举反例a=8,b=2,p=6就不满足。既然不能除,那咱们就乘呗,众所周知,除以一个数等于乘它的倒数,
所以,除法的模运算需要用到逆元。
假设要计算(x×2−1) % p,我们就要找2−1的逆元。
因为
2×2−1≡1 (mod p)
我们不妨令
2×2−1=p+1
就有
2−1=2p+1
因此,2p+1就是2−1的在mod p意义下的逆元
所以除法的模运算就是:
(a/b) % p=(a×b−1) % p=(a % p×b−1 % p) % p
其中b−1是b的逆元
逆Inverse
求解一般形式的同余方程ax≡b (mod m),需要用到逆(Inverse)
给定整数a,且满足gcd(a,m)=1,称ax≡1(mod m)的一个解为a模m的逆,记为a−1。
例如,8x≡1 (mod 31),丢番图方程:
8x+31y=1
有一个解是x=4,4是8模31的逆,因为4×8-1才能整除31。所有解,如35,66等,都是8模31的逆
扩展欧几里得算法 求单个逆
例题洛谷P1082,求解同余方程ax≡1 (mod m)
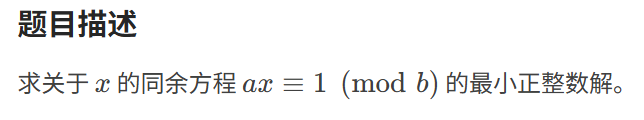

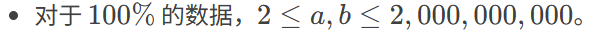
ax≡1 (mod m),即丢番图方程ax+my=1,用扩展欧几里得算法求出一个特解x0,通解就是x=x0+tm。再用((x0 mod m)+m) mod m求出最小正整数解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| #include <bits/stdc++.h>
using namespace std;
using ll = long long;
ll exgcd(ll a,ll b,ll &x,ll &y){
if(b == 0) {x = 1; y = 0; return a;}
ll d = exgcd(b,a%b,y,x);
y -= a/b * x;
return d;
}
ll inv(ll a,ll m){
ll x,y;
exgcd(a,m,x,y);
return (x%m + m) % m;
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
ll a,b;
cin >> a >> b;
cout << inv(a,b);
return 0;
}
|
线性求逆
模板题洛谷P3811
首先有i=1的逆是1。然后用递推求[1,n]内的所有逆,O(n)的时间复杂度
(1) 设ip=k,余数是r,即
k×i+r≡0 (mod p)
(2) 在等式两边乘i−1×r−1,得到
rk+i1≡0 (mod p)
(3) 移项得
i1≡−rk (mod p)
代入k=ip,得
i1≡−i×rp (mod p)
i1≡rp−ip (mod p)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| #include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int maxn = 3e6+5;
ll inv[maxn]{};
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
ll n,b;
cin >> n >> b;
inv[1] = 1;
cout << inv[1] << '\n';
for(int i=2;i<=n;i++){
inv[i] = ((b-b/i) * inv[b%i])%b;
cout << inv[i] << '\n';
}
return 0;
}
|