进阶搜索算法

回溯与剪枝

当递归所衍生出的子节点不符合条件时，就该“看到不对劲就撤退”——中途停止并返回。这个思路就是回溯。在回溯中用于减少子节点的拓展函数就是剪枝函数。

其难度主要在于拓展子节点的时候如何构造停止递归并返回的条件。

以HDU 2553 N皇后为例

题目

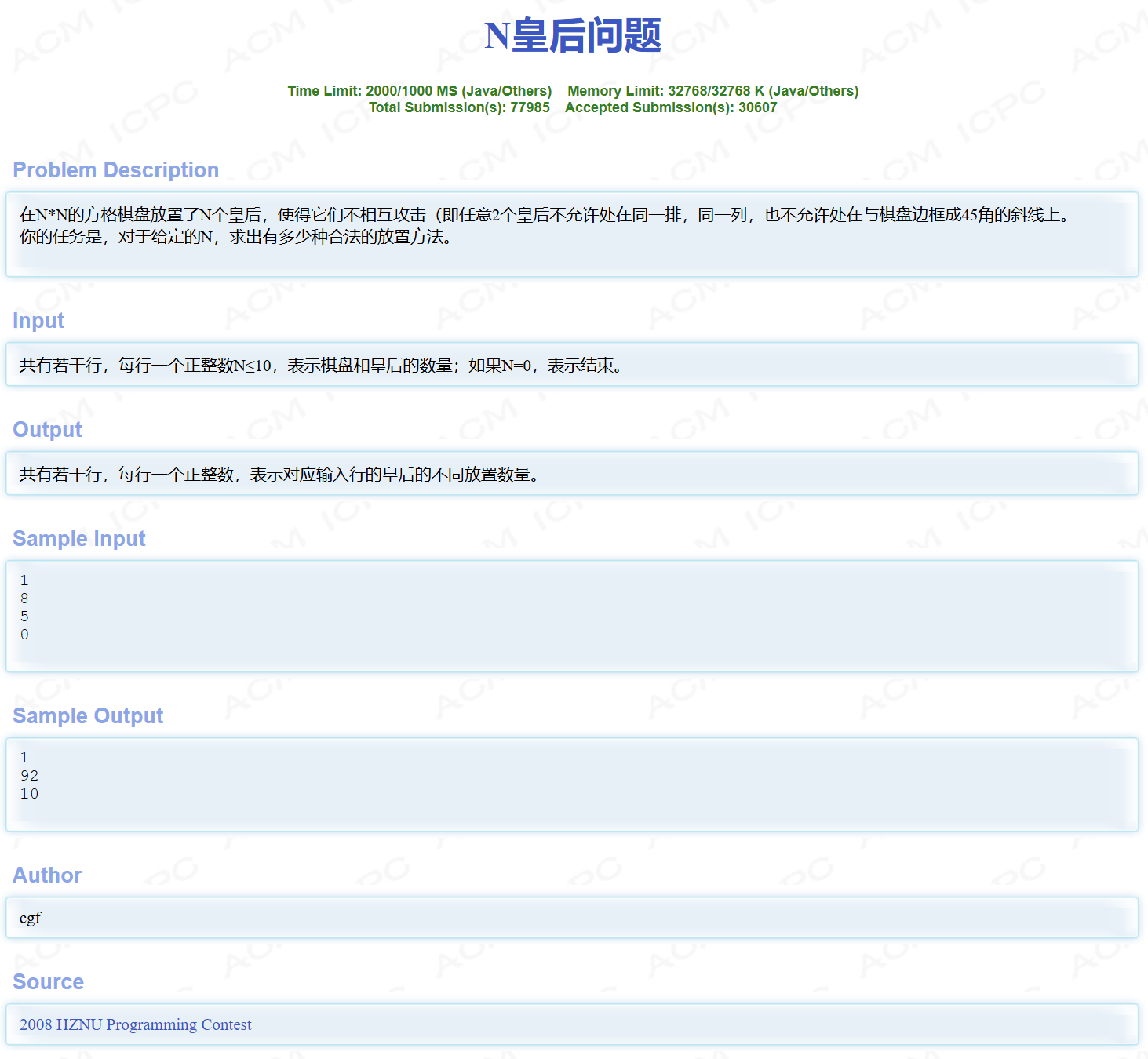
不同行: $old\_ x \not= new\_ x$

不同列: $old\_ y \not= new\_ y$

不同对角线: $abs(old\_ x - new\_ x) \not= abs(old\_ y - new\_ y)$

代码

#include <bits/stdc++.h>
using namespace std;

int n,lie[11],ans[11],sum;

bool check(int newx,int newy){            //剪枝函数 
    for(int i=0;i<newx;i++){
        if(lie[i]==newy || abs(i-newx)==abs(lie[i]-newy))
            return false;
    }
    return true;
}

void dfs(int newx){
    if(newx==n){
        sum++;
        return;
    }
    for(int newy=0;newy<n;newy++){
        if(check(newx,newy)){
            lie[newx]=newy;
            dfs(newx+1);
        }
    }
}
int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    for(n=0;n<=10;n++){				//对n=0~10打表 
        memset(lie,0,11);
        sum=0;
        dfs(0);
        ans[n]=sum;
    }
    while(cin >> n){
        if(n==0) return 0;
        cout << ans[n] << '\n';		//查表输出 
    }	
    return 0;
}

A*

A* 相当于是 BFS+贪心 ，是最短路里比较简单的一种算法。A*通常与曼哈顿距离扯上联系。

曼哈顿距离：两个点在标准坐标系上的实际距离，也称为出租车距离。

A*算法的一般性描述：在搜索过程中，用一个评估函数对当前情况进行评估，得到最好的状态，从这个状态继续搜索，直到目标。

以下是用A*算法来实现的八数码。manhadun()是评估函数，来评估某个状态里的每个数距离它的最终位置的距离之和，并把这个距离之和和这个状态对应的步数存进优先队列（小根堆）。

#include <bits/stdc++.h>
using namespace std;

string goal="123804765",start;
int explore[][2]={0,1,0,-1,1,0,-1,0},nextx,nexty,
goer[][2]={0,0,0,0,0,1,0,2,1,2,2,2,2,1,2,0,1,0};
#define check (nextx>=0 && nextx<3 && nexty>=0 && nexty<3)
int manhadun(string s){
    int sum=0;
    for(int i=0;i<9;i++){
        int t = s[i]-'0';
        if(t) sum += abs(i/3-goer[t][0])+abs(i%3-goer[t][1]);
    }
    return sum;
}
int astar(string s){
    unordered_map <string,int> um;
    priority_queue <pair<int,string>> q;
    q.push({-manhadun(s),s});um[s]=0;
    while(!q.empty()){
        auto a=q.top();q.pop();
        string st = a.second;
        if(st==goal) return um[st];
        int Index = st.find('0');
        int x=Index/3,y=Index%3;
        for(int i=0;i<4;i++){
            nextx=x+explore[i][0];nexty=y+explore[i][1];
            if(check){
                string t=st;
                swap(t[Index],t[nextx*3+nexty]);
                if(!um.count(t)){
                    um[t]=um[st]+1;
                    q.push({-(um[t]+manhadun(t)),t});
                }
            }
        }
    }
}
int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> start;
    cout << astar(start) << '\n';
    return 0;
}

迭代加深搜索 IDDFS

当搜索树深度极深，宽度极广，DFS陷入递归无法返回、BFS队列空间直接爆炸，此时就可以采取迭代加深搜索 IDDFS

IDDFS结合了DFS和BFS。迭代过程上，在每一层的广度上采用了BFS，在具体实现上是DFS，大概的操作是：

1. 先设定搜索深度为1,用DFS搜索到第1层即停止。也就是说，用DFS搜索一个深度为1的搜索树。

2. 如果没有找到答案，再设定深度为2,用 DFS 搜索前两层即停止。也就是说，用DFS搜索一个深度为2的搜索树。

3. 继续设定深度为3、4……逐步扩大 DFS的搜索深度，直到找到答案。

以 埃及分数 为例

题目

该题的搜索树深度和宽度都可能是无穷的，所以要用IDDFS

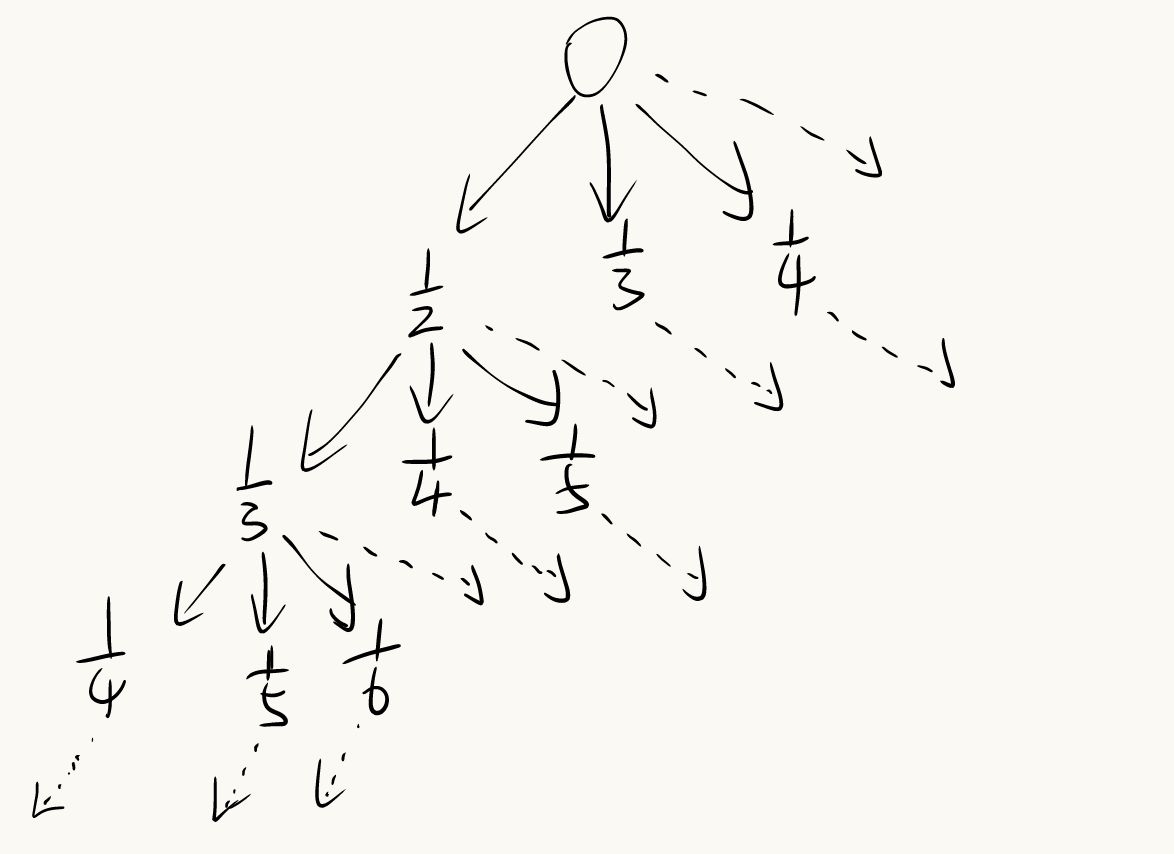
这一层找到了就不会去下一层找了，所以ans和temp的分母数量是相同的,也就是该层的层数

每一层搜索分母的起始值为i=b/a+1，i是分母，+1是因为找的分数要比题目给的分数小

每一层搜索分母的时候也有个限度，不可能无限搜吧，这个限度就是：

如果 剩余分母个数/分母 < 题目给的分数 ，即(deep-d+1)/i < a/b，那么这层就不用搜了，因为这层剩下的分数之和的最大值就是(deep-d+1)/i，如果这小于a/b了，那么这层分数再怎么累加也比a/b小。可以放缩证明，证明如下：

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 1e7;
int ans[maxn+2],temp[maxn+2],pd=0,deep;

int gcd(int a,int b){                    //欧几里得 
    return (b==0 ? a:gcd(b,a%b));
}

void simp(int &a,int &b){                //分数化简 
    int gys=gcd(a,b);
    a=a/gys;
    b=b/gys;
}

void iddfs(int a,int b,int d){
    //cout << "abc" << endl;
    if(d==deep){
        if(b%a) return;					//分子不为1，剪掉 
        if(temp[deep-1]==b/a) return; 	//分母重复，剪掉 
        pd=1;							//表示找到了 
        temp[d]=b/a;
        int pd1=0;
        if(ans[d]>temp[d]) memcpy(ans,temp,sizeof(int)*(d+1));
        return;
    }
    for(int i=max(temp[d-1]+1,b/a+1);;i++){	//i表示分母 
        if(b*(deep-d+1)<a*i) break;			//这不能用除法来判断，会陷入死循环(整除的原因); 
        temp[d]=i;
        // a/b-1/i=......
        //通分: (a*i-b)/b*i=......
        int a_1=a*i-b,b_1=b*i; 
        simp(a_1,b_1);
        iddfs(a_1,b_1,d+1);
    }
} 
signed main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int a,b;
    cin >> a >> b;
    simp(a,b);
    if(!b%a) cout << b/a << '\n';
    else{
        for(deep=2;;deep++){
            ans[1]=0,ans[deep]=maxn;	//初始化。要的是分母小的，所以最后一项先赋值最大，方便比较 
            iddfs(a,b,1);
            if(pd) break; 
        }
        for(int i=1;i<=deep;i++) cout << ans[i] << ' ';
        cout << '\n';
    }
    return 0;
} 

Dijkstra

迪杰斯特拉简单概括为 BFS+贪心，是一种单源最短路算法，一次计算能得到从一个起点到其它所有点的最短距离长度、最短路径的途径点。注意，dijkstra不能做边权为负数的题目。
Dijkstra的核心思想是：每次从未访问过的点中，选择距离起点最近的点作为新的起点。
Dijkstra的复杂度：设图有 $n$ 个点， $m$ 条边。稀疏图复杂度为 $O((m+n)log_2n)$ ，但是在稠密图的情况下复杂度会上升到 $O(n^2log_2n)$ 。

来看看具体做法吧：

---

1. 从起点 $s$ 出发，用BFS扩展它的邻居节点，把这些邻居节点放到一个集合 $A$ 中，并记录这些点到起点 $s$ 的距离。
2. (1) 在集合 $A$ 中选择距离起点最近的点 $v$，作为新的起点，然后用BFS扩展它的邻居节点，把这些邻居节点放到集合 $A$ 中
   (2) 如果 $v$ 的邻居经过 $v$ 的中转，到 $s$ 的距离更短，就更新这些邻居到 $s$ 的距离
   (3) 从集合 $A$ 中移除 $v$ ，后续不再处理它
3. 重复第2步，直到集合 $A$ 为空。

---

模板题：

#include <bits/stdc++.h>
using namespace std;
const long long INF = 0x3f3f3f3f3f3f3f3fLL; //这样定义的好处是INF <= INF+x 
const int N = 3e5+2;

struct edge{
    int from, to; //边：起点，终点，权值；起点from并没有用到，e[i]的i就是from 
    long long w; //权值 
    edge(int a,int b,long long c) : from(a),to(b),w(c) {}
};

vector <edge> e[N];  //邻接表存图 

struct node{
    int id; long long n_dis; //id：节点；n_dis：这个节点到起点的距离 
    node(int b,long long c){id = b;n_dis = c;}
    bool operator < (const node & a) const 
    {return n_dis > a.n_dis;}
};

int n,m;
int pre[N]; //记录前驱节点 

void print_path(int s,int t){ //打印s到t的最短路径 
    if(s == t) {cout << s << '\n';return;} //打印起点 
    print_path(s,pre[t]); //先打印前一个点 
    cout << t << '\n'; //后打印当前点，最后打印终点t 
}

long long dis[N]; //记录所有节点到起点的距离 
bool done[N]; //true表示节点i已经访问过 

void dijkstra(){
    int s = 1; //起点s=1 
    for(int i=1;i<=n;i++){dis[i] = INF;done[i] = false;} //初始化 
    dis[s] = 0; //起点到自己的距离为0 
    priority_queue <node> q; //优先队列，存节点信息
    q.push({s,dis[s]});
    while(!q.empty()){
        node u = q.top(); //弹出离起点s距离最小的点u 
        q.pop();
        if(done[u.id]) continue;
        done[u.id] = true;
        for(edge v:e[u.id]){ //访问节点u的所有邻居 
            if(done[v.to]) continue;
            if(dis[v.to] > u.n_dis + v.w){  
                dis[v.to] = u.n_dis + v.w;
                q.push({v.to,dis[v.to]}); //拓展新邻居，加入队列 
                pre[v.to] = u.id; //记录新邻居v的前驱为u 
            }
        }
    }
    //print_path(s,n) 	//如有需要就打印s到n的最短路径 
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n >> m;
    for(int i=0;i<m;i++){
        int u,v,w;
        cin >> u >> v >> w;
        e[u].push_back({u,v,w});
        //e[v].push_back({u,w});	//这道模板题是单向边 
    }
    dijkstra();
    for(int i=1;i<=n;i++){
        if(dis[i]>=INF) cout << "-1 ";
        else cout << dis[i] << ' ';
    }
    cout << '\n';
    return 0;
}