01背包
(这只是正式开始学习背包，但是由于做题的原因，之前已经接触了一些背包问题、零零散散地学了一些了)
01背包问题通常为：给定 n 种物品和一个背包，第 i 个物品体积为 ci ，价值为 wi ，背包地容量为 C 。如何选择装入背包的物品，使装入背包中的物品的总价值最大？
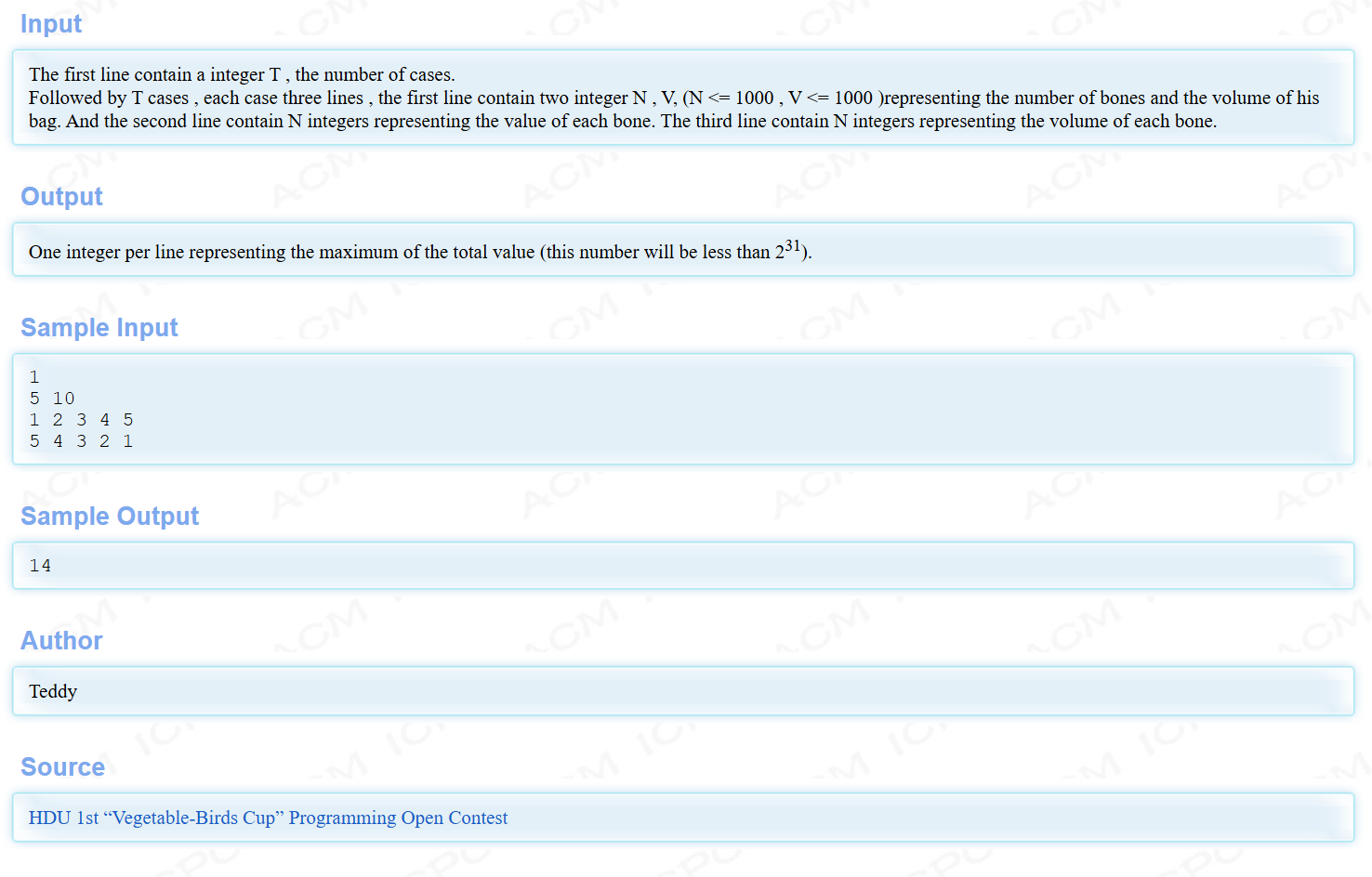
以 HDU 2602 为例
题目
用自底向上的递推完成转移过程， dp[i][j] 表示把前 i 个物品(从第 1 个到第 i 个)装入容量为 j 的背包中获得的最大价值。假设现在递推到 dp[i][j] ，分两种情况：
(1) 第 i 个物品的体积比 j 还大，则不能装入当前背包，直接继承前 i−1 个物品装入容量为 j 的背包，即
dp[i][j]=dp[i−1][j]
(2) 第i个物品体积比j小，能装进背包，又分为两种：装或不装
取①②中的最大值，状态转移方程为
dp[i][j]=max(dp[i−1][j−c[i]]+w[i],dp[i−1][j])
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include <bits/stdc++.h>
using namespace std;
const int N = 1001;
int w[N],c[N],dp[N][N];
int solve(int n,int C){
for(int i=1;i<=n;i++)
for(int j=0;j<=C;j++){
if(c[i] > j) dp[i][j] = dp[i-1][j];
else dp[i][j] = max(dp[i-1][j],dp[i-1][j-c[i]]+w[i]);
}
return dp[n][C];
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n,C;
cin >> n >> C;
for(int i=1;i<=n;i++)
cin >> w[i];
for(int i=1;i<=n;i++)
cin >> c[i];
memset(dp,0,sizeof(dp));
cout << solve(n,C) << '\n';
}
return 0;
}
|
滚动数组–dp空间优化
dp状态方程常常是二维以上的，占用空间多。从状态方程
dp[i][j]=max(dp[i−1][j−c[i]]+w[i],dp[i−1][j]) 可以看出， dp[i][] 只与 dp[i−1][] 有关，所以就用新的一行覆盖已经无用的一行(滚动)，只需要两行就够了。
1
2
3
| for(int i=1; i<=n; i++}
for(int j=C; j>=c[i]; j--)
dp[j] = max( dp[j], dp[j-c[i]] + w[i] );
|
要注意：j 应该反过来循环，即从后向前覆盖，否则同一个物品可能会被装两次
优化后DP的空间复杂度从 O(N×C) 降低到 O(C)
话不多说，来一道题
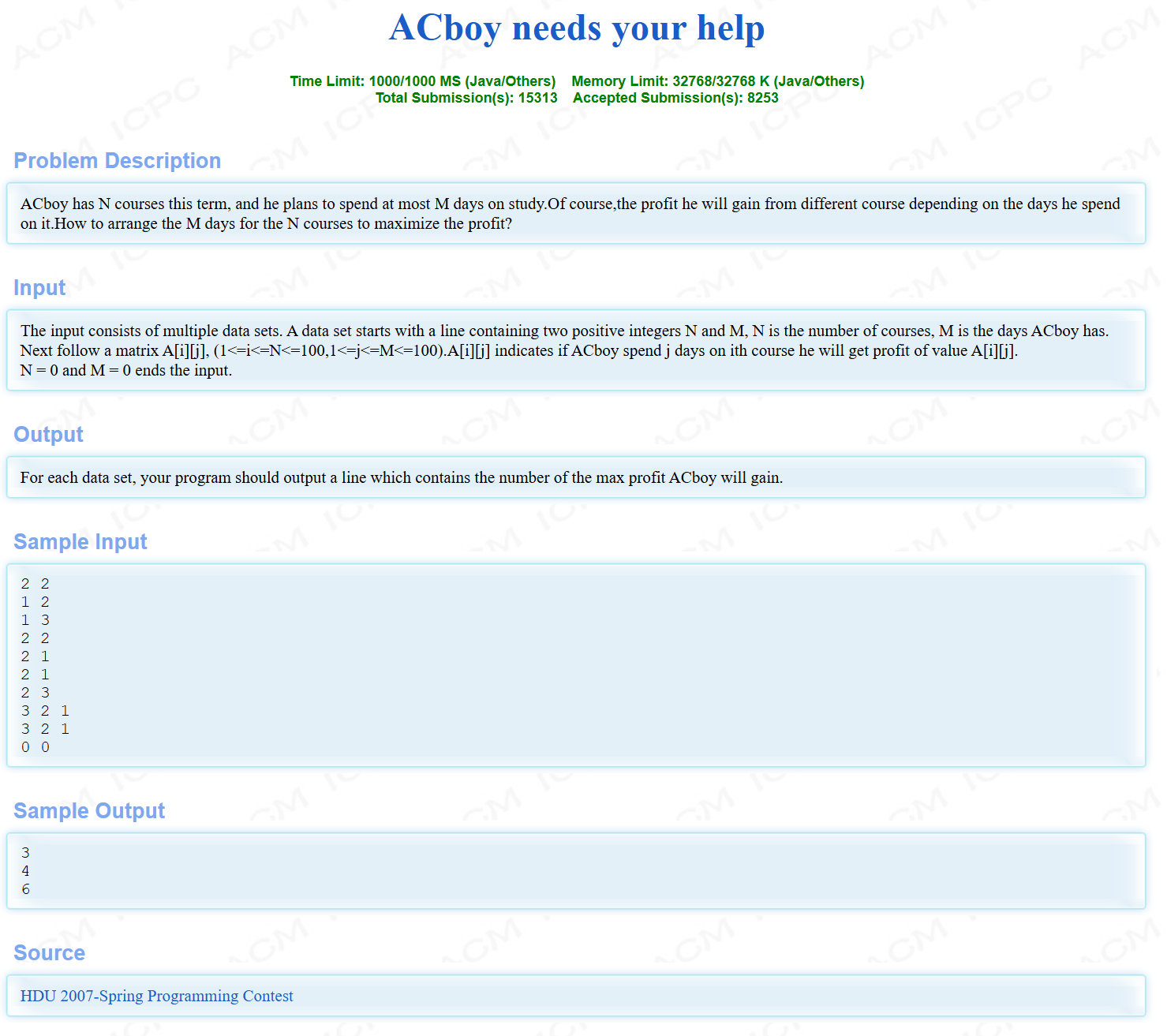
题目
这道题是分组背包，需要三层循环
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| #include <bits/stdc++.h>
using namespace std;
int dp[101],c[101][101];
void read(int N,int M){
memset(c,0,sizeof(c));
for(int i=1;i<=N;i++)
for(int j=1;j<=M;j++)
cin >> c[i][j];
}
int solve(int N,int M){
memset(dp,0,sizeof(dp));
for(int i=1;i<=N;i++)
for(int j=M;j>=0;j--)
for(int k=1;k<=M;k++)
if(j>=k)
dp[j]=max(dp[j],dp[j-k]+c[i][k]);
return dp[M];
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int N,M;
cin >> N >> M;
while(N || M){
read(N,M);
cout << solve(N,M) << '\n';
cin >> N >> M;
}
return 0;
}
|
状压DP
状压DP是DP的一种优化方法
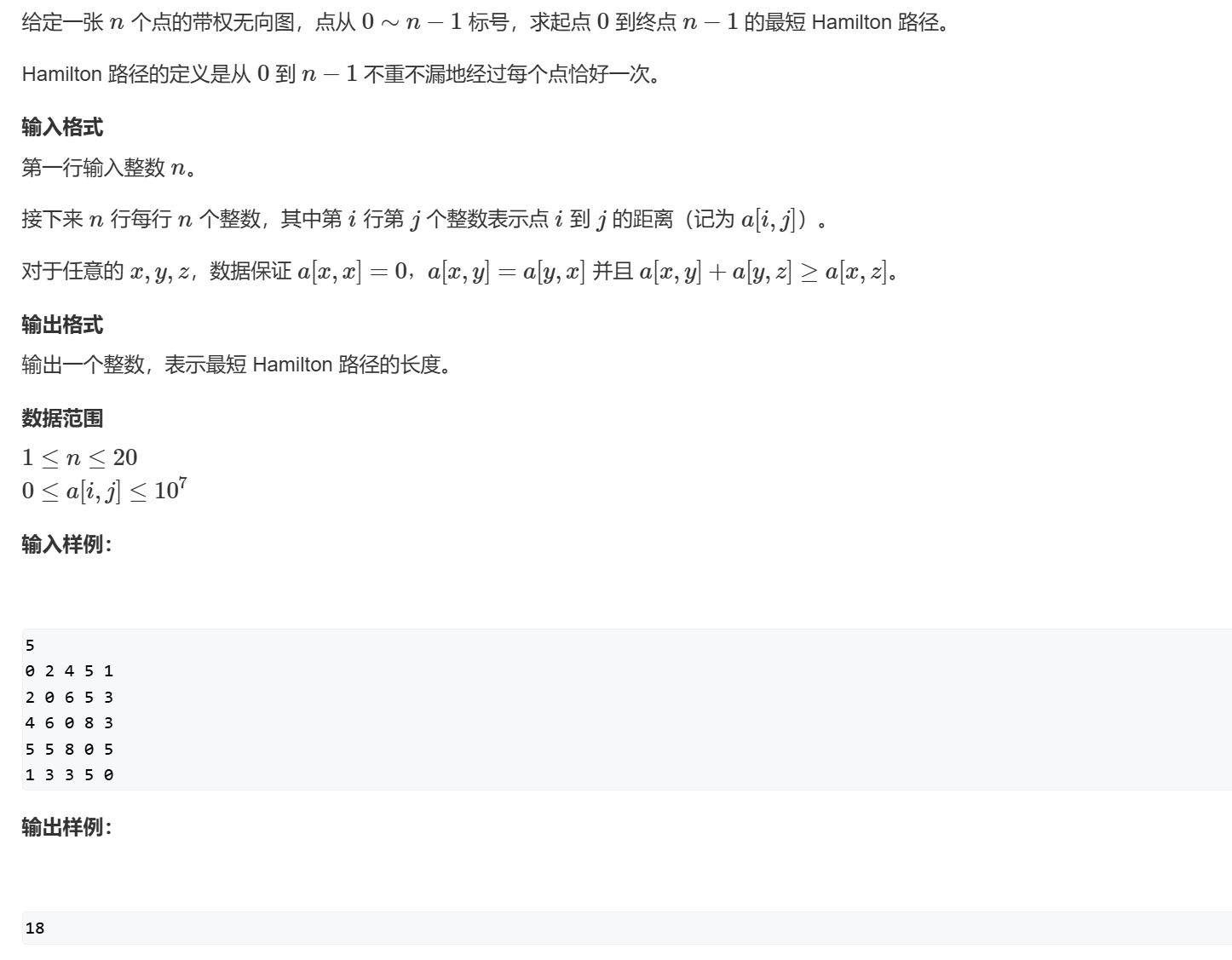
Hamilton旅行商问题
Hamilton问题是NP问题，没有多项式复杂度的解法，暴力解法复杂度是 O(n×n!) ，而状压DP可将复杂度将为 O(n2×2n)
设 S 为图的一个子集；
dp[S][j] ：表示“集合 S 内的最短Hamilton路径”，即从起点 0 出发经过 S 中所有点，到达终点 j 时的最短路径；集合 S 中包括 j 点；
让 S 从最小的子集逐步拓展到整个图，最后得到的 dp[N][n−1] 就是答案， N 表示包含图上所有点的集合。
（ S−j 表示从集合 S 中去掉 j ，即不包含 j 点的集合）
设 k 为 S−j 中一个点，把从 0 到 j 的路径分为两部分：(0→⋯→k)+(k→j) 。以 k 为变量枚举 S−j 中所有的点，找出最短路径
状态转移方程为：
dp[S][j]=min(dp[S−j][k]+dist(k,j))
状态压缩DP的技巧：用一个二进制数表示集合 S ，即把 S 压缩到一个二进制数中， S 的每一位表示图上的一个点， 0 表示不包含， 1 表示包含
例如 S=00000101 ，表示包含 2，0 这两个点
if((S>>j) & 1)，判断当前的集合 S 中是否含有 j 点
if((S^(1<<j))>>k & 1) ,其中S^(1<<j)的作用是从集合中去掉 j 点，得到集合 S−j ，然后>> k & 1表示用 k 遍历集合中的 1 ，这些 1 就是 S−j 中的点，这样就实现了"枚举集合 S−j 中所有的点" (S^(1<<j))也可以写成S-(1<<j)
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| #include <bits/stdc++.h>
using namespace std;
int n,dp[1<<20][21];
int dist[21][21];
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
memset(dp,0x3f,sizeof(dp));
cin >> n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
cin >> dist[i][j];
dp[1][0] = 0;
for(int S=1;S<(1<<n);S++)
for(int j=0;j<n;j++)
if((S>>j) & 1)
for(int k=0;k<n;k++)
if((S^(1<<j)) >> k & 1)
dp[S][j] = min(dp[S][j],dp[S^(1<<j)][k] + dist[k][j]);
cout << dp[(1<<n)-1][n-1] << '\n';
return 0;
}
|
树形DP
首先是树的储存，树的储存是图的储存的特殊情况，可以用邻接表储存，或链式向前星
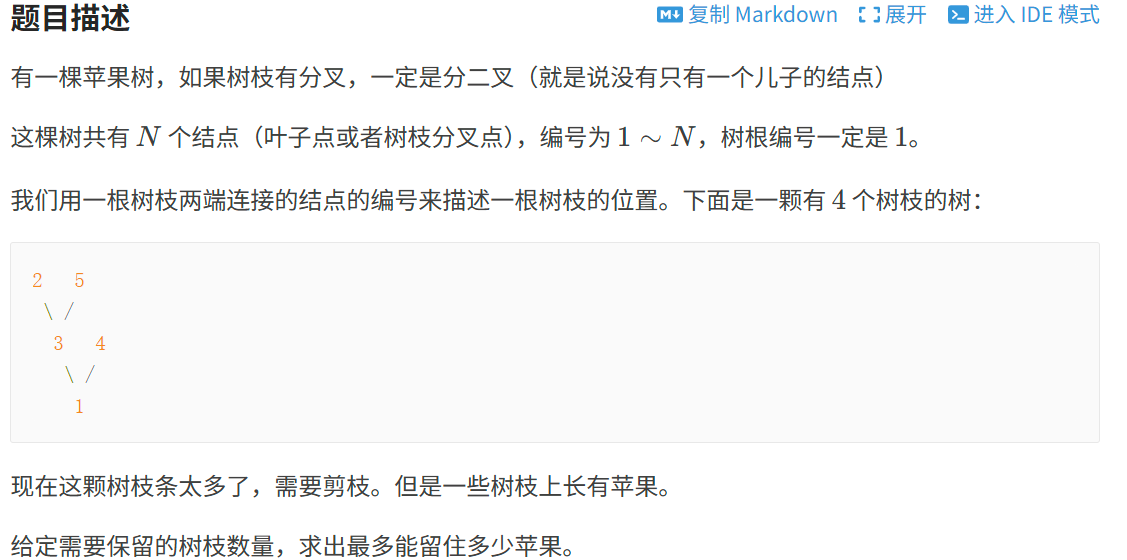
二叉苹果树
洛谷P2015
定义状态 dp[u][j] 表示以节点 u 为根的子树上留 j 条边时的最多苹果数量。 dp[1][q] 就是答案。
状态转移方程:
dp[u][j]=max(dp[u][j],dp[u][j−k−1]+dp[v][k]+w)
其中，v 是 u 的一个子节点。 dp[u][j] 的计算分以下两部分：
- dp[v][k] ：在 v 上留 k 条边
- dp[u][j−k−1] ：除了 v 上的 k 条边，以及 u−v 边，那么以u为根的这棵树上还有 j−k−1 条边，它们在 u 的其他子节点上
总复杂度小于 O(n3)
PS：
- 这道题是无向图储存，因为题目没有说明输入的两个节点哪个是爹哪个是儿，所以要
push_back两次，然后在搜的时候跳过father
- j 循环必须递减，例如 dp[u][5] 会用到 dp[u][4] 和 dp[u][3] 等等，若是递减循环，先算 5 ，再算 4 ，再算 3 … dp[u][5] 用到的是 dp[u][4] 和 dp[u][3] 的原值；若是递增循环， dp[u][5] 就会用到 dp[u][4] 和 dp[u][3] 的新计算后的值，就不对了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| #include <bits/stdc++.h>
using namespace std;
const int N = 200;
int n,q;
int dp[N][N], sum[N];
struct node{
int v,w;
node(int a,int b) : v(a),w(b) {}
};
vector <node> e[N];
void dfs(int u,int father){
for(auto i:e[u]){
if(i.v == father) continue;
dfs(i.v,u);
sum[u] += sum[i.v]+1;
for(int j=min(q,sum[u]);j>=0;j--)
for(int k=0;k<=min(sum[i.v],j-1);k++)
dp[u][j] = max(dp[u][j], dp[u][j-k-1] + dp[i.v][k] + i.w);
}
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin >> n >> q;
for(int i=1;i<n;i++){
int u,v,w;
cin >> u >> v >> w;
e[u].push_back({v,w});
e[v].push_back({u,w});
}
dfs(1,0);
cout << dp[1][q];
return 0;
}
|
没有上司的舞会
典，上图
这题和上题有点区别
这题没有定义结构体，因为这题是有向无权图，题目已经表明了输入的节点中哪个是爹哪个是儿，而且没有边上没有权值。
定义状态 dp[u][0] 表示不选择当前节点的最优解， dp[u][1] 表示选择当前节点的最优解。
状态转移方程：
dp[u][1]+=dp[v][0]
表示选择该节点，就累加上不选子节点的最大值
dp[u][0]+=max(dp[v][0],dp[v][1])
表示不选该节点，子节点可选可不选
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| #include <bits/stdc++.h>
using namespace std;
const int N = 6666;
int n, dp[N][2], w[N], father[N];
vector <int> e[N];
void dfs(int u){
dp[u][0] = 0;
dp[u][1] = w[u];
for(auto v:e[u]){
dfs(v);
dp[u][1] += dp[v][0];
dp[u][0] += max(dp[v][0], dp[v][1]);
}
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin >> n;
for(int i=1;i<=n;i++) cin >> w[i];
for(int i=1;i<n;i++){
int u,v;
cin >> v >> u;
e[u].push_back(v);
father[v] = u;
}
int t = 1;
while(father[t]) t = father[t];
dfs(t);
cout << max(dp[t][0], dp[t][1]) << '\n';
return 0;
}
|
区间DP
石子合并
以一道模板题目为例----石子合并
不能用贪心，会陷入局部最优解。用DP求解
定义 dp[i][j] 为合并第 i 堆到第 j 堆的最小花费
状态转移方程为：
dp[i][j]=min(dp[i][k]+dp[k+1][j]+w[i][j])， i≤k<j
w[i][j] 表示第 i 堆到第 j 堆的石子总数，可以用前缀和计算。dp[1][n] 就是答案
复杂度 O(n3) ，可以用四边形不等式优化到 O(n2)
自顶向下的思路：
计算大区间 [i,j] 的最优值时，合并它的两个子区间 [i][k] 和 [k+1][j]，对所有可能的合并 (i≤k<j) 采取最优合并。子区间再分解为更小的区间，最小区间 [i,i+1] 只包含两堆石子
自底向上的编程：
先在小区间进行DP得到最优解，再逐步合并小区间为大区间。以下是code：
1
2
3
4
5
6
7
8
9
10
11
12
| const int INF = 0x3f3f3f3f;
int dp[n][n] {};
for(int len = 2; len <= n; len++){
for(int i = 1; i <= n - len + 1; i++){
int j = i + len - 1;
dp[i][j] = INF;
for(int k = i; k < j; k++){
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j] + sum[j] - sum[i-1]);
}
}
}
|
字符串区间
大致题意：两个长度相等的小写字母字符串 A 和 B 。定义一次操作：把 A 的一个连续子串（区间）都转换为某个字符串（就像用刷子刷成一样的字符）。要把 A 转换成 B ，所需最少操作数是多少？ strlen≤100
input：
zzzzzfzzzzz
abcdefedcba
output:
6
两部分dp：1.从空白串转换到 B 。2.从 A 转换到 B
- 从空白串转换到 B ：
① B[i]==B[j] ，原区间 [i,j] 的最少操作次数 等于 分别去掉两个端点的区间的最少操作次数，例如 B=abbba ，最少刷两遍，第一遍刷 aaaaa ，第二遍刷 bbb ；去掉头变为 bbba ，也要刷两遍；去掉尾变 abbb ，也要刷两遍。
② B[i]=B[j] ，用标准的区间操作，把区间分为 [i,k] 和 [k+1,j] 两部分来dp
- 从A转换到B
① A[j]==B[j] ，不用转换，有 dp[1][j]=dp[1][j−1]
② A[j]=B[j] ，用标准的区间操作，把区间分为 [i,k] 和 [k+1,j] 两部分来dp；这里利用了从空白串转化为 B 的结果，当区间 [k+1,j] 内的A和B字符不同时，从A转化到B与从空白串转化到B是一样的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include <bits/stdc++.h>
using namespace std;
const int inf = 0x3f3f3f3f;
int dp[102][102];
string a,b;
void solve(const int& n){
for(int len=2;len<=n;len++){
for(int i=1;i<=n-len+1;i++){
int j = i+len-1;
dp[i][j] = inf;
if(b[i] == b[j])
dp[i][j] = dp[i+1][j];
else for(int k = i;k < j;k++)
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j]);
}
}
for(int j=1;j<=n;j++){
if(a[j] == b[j])
dp[1][j] = dp[1][j-1];
else for(int k=1;k<j;k++)
dp[1][j] = min(dp[1][j], dp[1][k] + dp[k+1][j]);
}
cout << dp[1][n] << '\n';
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
while(cin >> a && cin >> b){
int n = a.size();
a = ' ' + a;
b = ' ' + b;
for(int i=1;i<=n;i++) dp[i][i] = 1;
solve(n);
}
return 0;
}
|
