codeforces 993 div4

A

题目

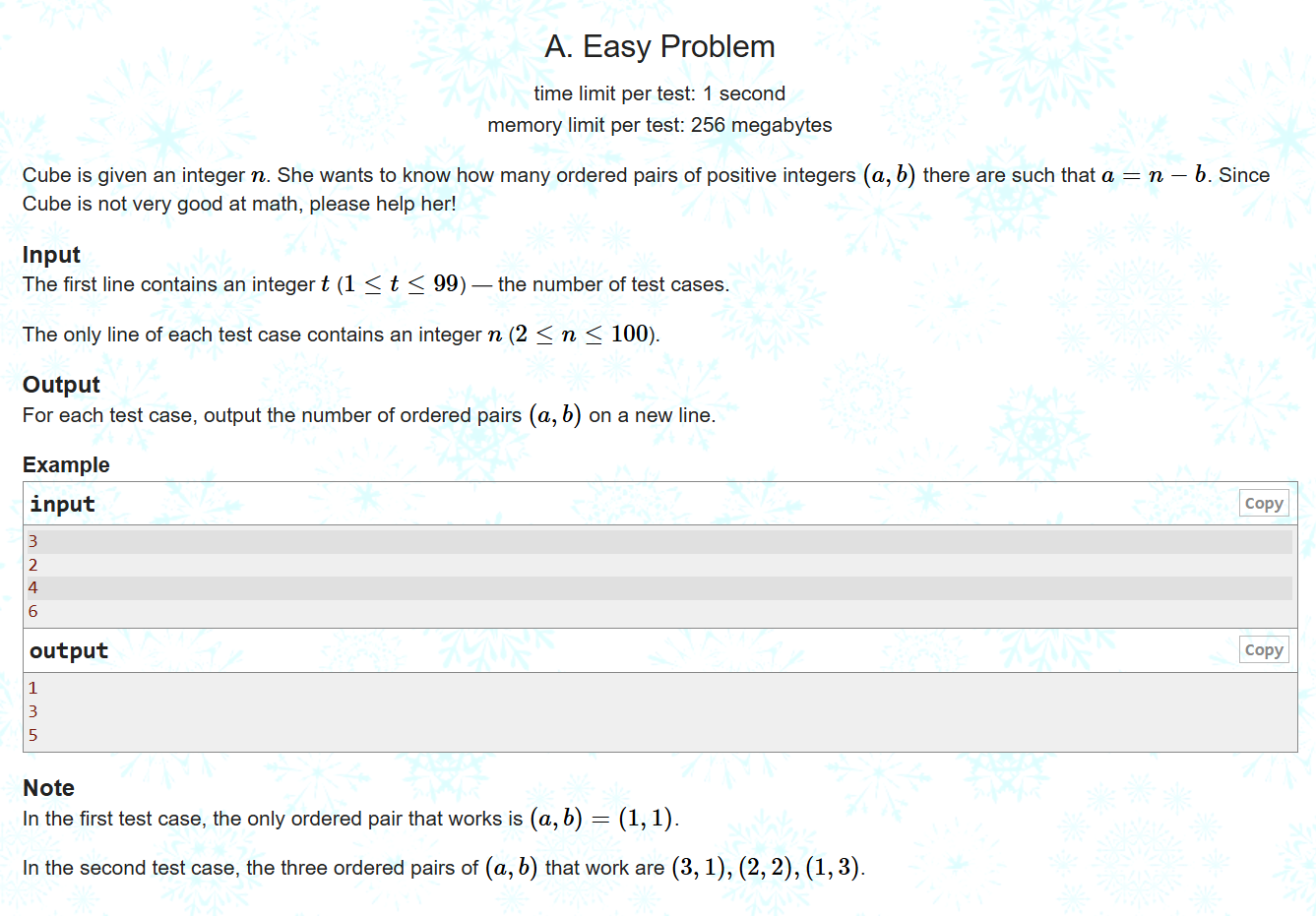
给你一个n，问你有多少有序数对(a,b)满足a+b=n？

其实就是n-1

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <bits/stdc++.h>
using namespace std;

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t,n;
    cin >> t;
    while(t--){
        cin >> n;
        cout << n-1 << '\n';
    }
    return 0;
}

B

题目

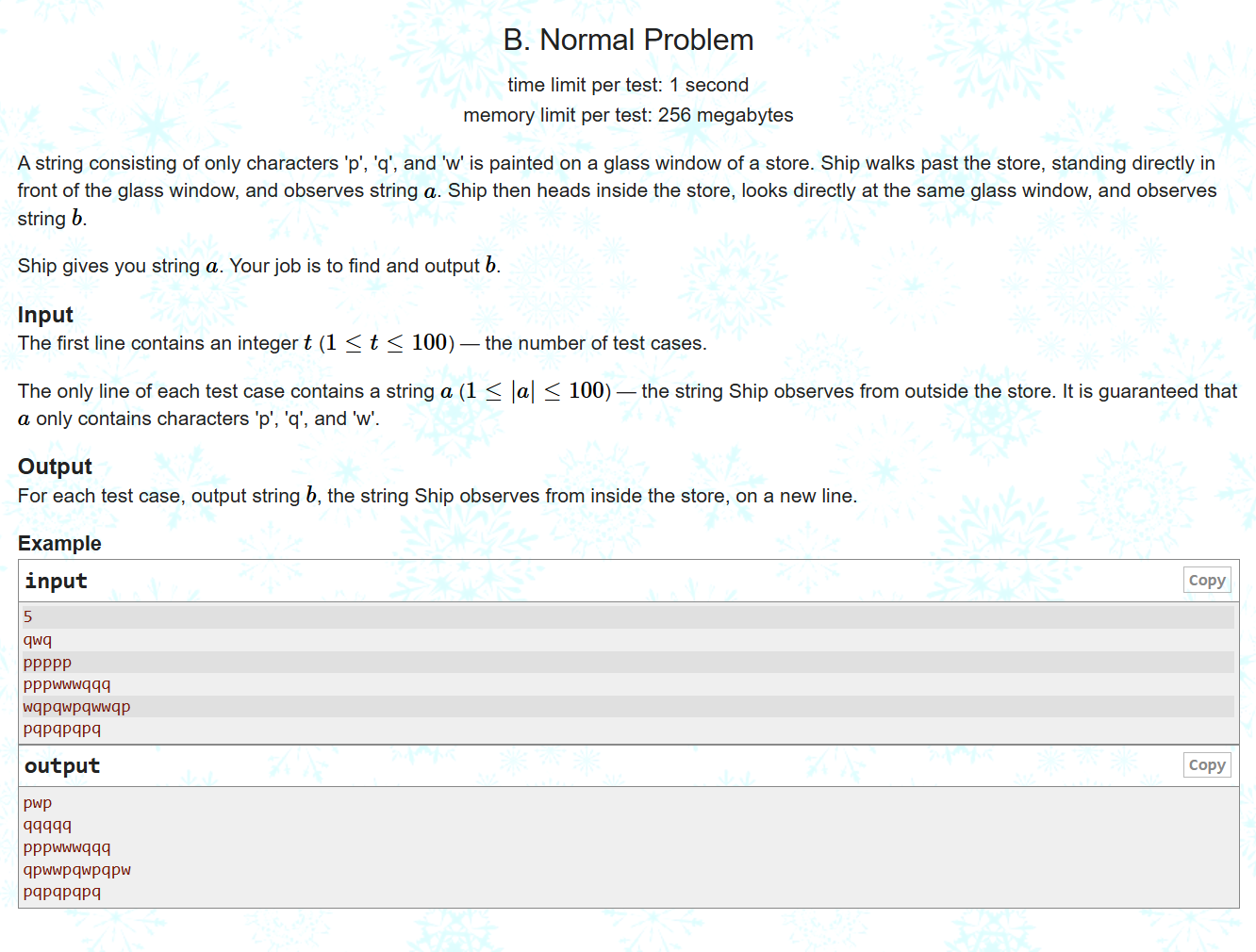
这个人在店铺外面看窗上的字母是"qwq"，问你在店铺里面看窗子上是什么字母?

逆序输出，q变p，p变q，w不变

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <bits/stdc++.h>
using namespace std;

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    string s;int t;
    cin >> t;
    while(t--){
        cin >> s;
        for(int i=s.size()-1;i>=0;i--){
            if(s[i]=='q') cout << 'p';
            else if(s[i]=='p') cout << 'q';
            else cout << 'w';
        }
        cout << '\n';
    }	
    return 0;
}

C

题目

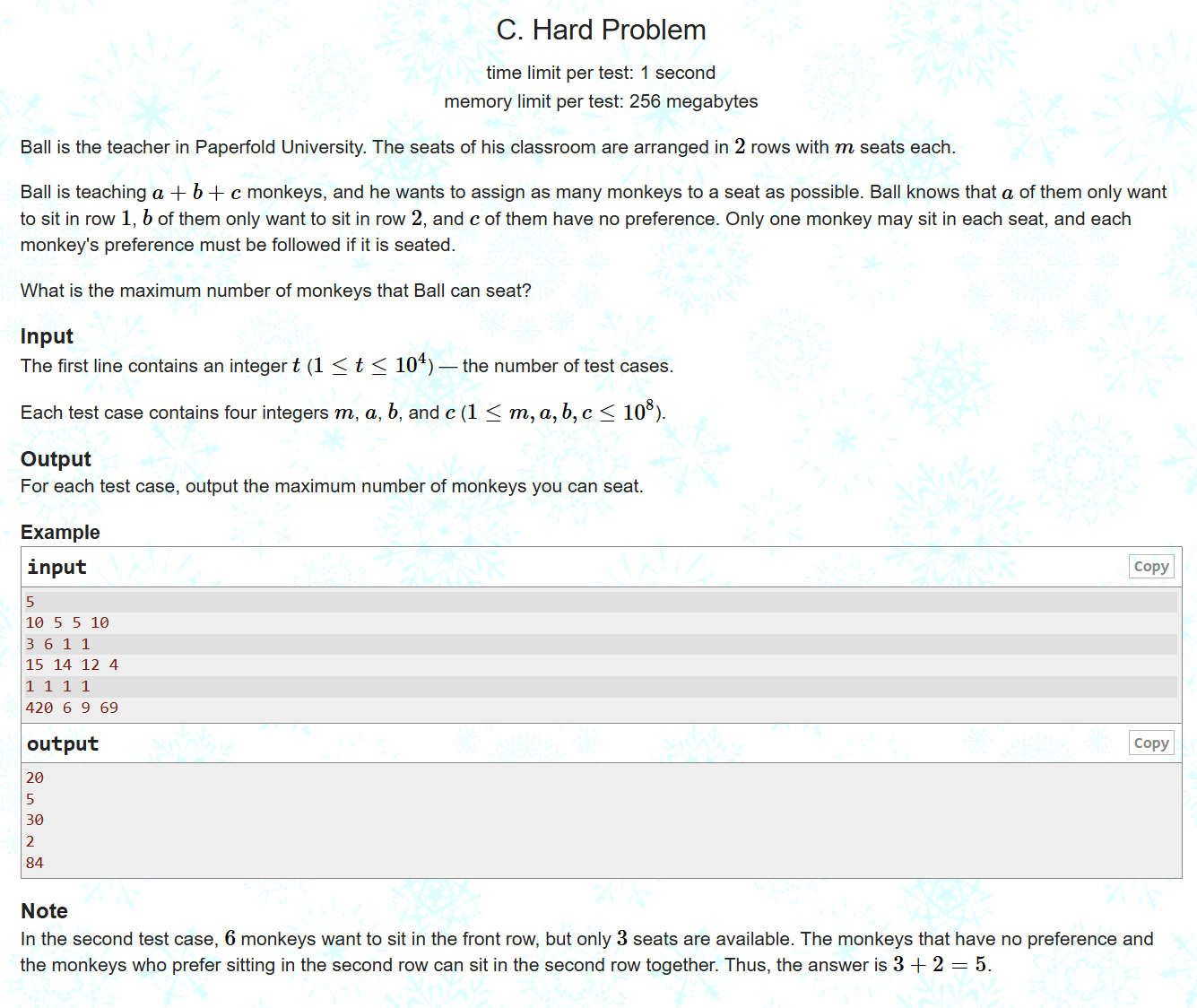
排2排座位，这两排座位总数相等。有a个人想坐第一排，有b个人想坐第二排，有c个人坐哪无所谓，但是座位是有限的，问你最多能坐多少人

这道题没有思维障碍，模拟题，用min()判断可以大幅减少代码

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <bits/stdc++.h>
using namespace std;

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t,m,a,b,c;
    cin >> t;
    while(t--){
        int res=0,z1,z2,sum=0;
        cin >> m >> a >> b >> c;
        z1=z2=m;
        sum+=min(m,a);sum+=min(m,b);
        if(m>=a) res+=m-a;
        if(m>=b) res+=m-b;
        sum += min(res,c);
        cout << sum << '\n';
    }
    return 0;
}

D

题目

构造题，给出一个n(数组长度)和一个数组a，你需要构造一个数组b，使得对于每个ai（1 <= i <=n） ，在数组b的前i个数里出现次数最多

让每个数最多出现一次，这样每个数都是出现次数最多的那个数。当轮到ai的时候，如果ai已经出现过了，那么就用其他没有出现过的数来代替

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <bits/stdc++.h>
using namespace std;
const int maxn=2e5+2;

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t;
    cin >> t;
    while(t--){
        int cache,Visit[maxn]={0},times=0,n;
        cin >> n;
        for(int i=0;i<n;i++){
            cin >> cache;
            if(!Visit[cache]){
                cout << cache << ' ';
                Visit[cache]=1;
            }
            else times++;
        }
        for(int i=1;times>0;i++){
            if(Visit[i]) continue;
            cout << i << ' ';
            times--;
        }
        cout << '\n';
    }
    return 0;
}

E

题目

给你k，l1，r1，l2，r2，问你在l1<=x<=r1 , l2<=y<=r2里面有多少是满足y/x=kn的？

思维题，一开始用的枚举去做，喜提TLE

后来改用二分，找每个n下面的xmin和xmax，sum+=xmax-xmin+1，过了

注意一下二分端点的判定，我是将l-1，r+1，扩大端点。这里调试了好久

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <bits/stdc++.h>
#define int long long
using namespace std;

signed main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t,k,l1,r1,l2,r2;
    cin>>t;
    while(t--){
        cin>>k>>l1>>r1>>l2>>r2;
        int k1=1,l=l1-1,r=r1+1,xmin,xmax,sum=0;	//为防止l和r相邻而进不了循环，而将l-1、r+1 
        while(k1<=r2){
            for(int mid;l+1<r;){
                mid=(l+r)/2;
                if(mid*k1<l2) l=mid;
                else r=mid;
            }//cout << "xmin:"<<r<<'\n';
            xmin=r,l=l1-1,r=r1+1;
            for(int mid;l+1<r;){
                mid=(l+r)/2;
                if(mid*k1<=r2) l=mid;
                else r=mid;	
                //cout<<"K:"<<k1<<' '<<"l:"<<l<<' '<<"r:"<<r<<'\n';
            }//cout << "xmax:"<<l<<'\n';
            xmax=l,k1*=k,l=l1-1,r=r1+1;
            sum += (xmax>=xmin?xmax-xmin+1:0);
        }
        cout << sum << endl;
    }
    return 0;
}

牛客108

A

题目

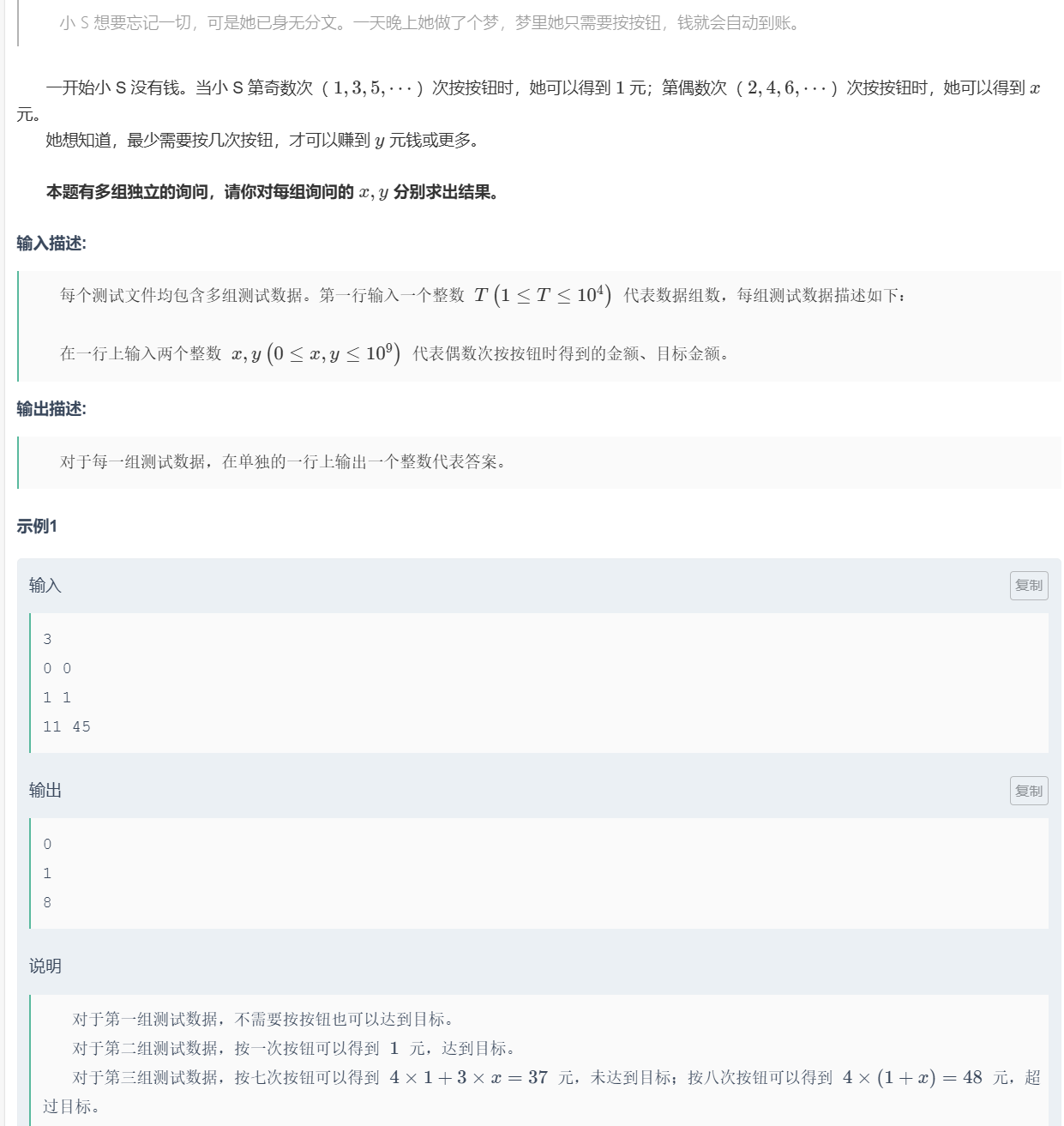
前不久才做了和这题很类似的cf的题（不是吧，牛客小白赛的A就有cf div3 B的水平了）对给的数进行处理，2个一组，先整除，再取模，对取的模进行处理

这题x、y可以等于0，有特判

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <bits/stdc++.h>
#define int long long
using namespace std;

signed main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t;
    cin >> t;
    while(t--){
        int x,y;
        cin >> x >> y;
        if(x==0 && y){
            if(y==1) cout << 1 << '\n';
            else cout << 2*(y-1)+1 << '\n';
        }
        else{
            int sum = 1+x;
            int day1 = 2*(y/sum);
            if(y%sum){
                int res = y%sum;
                if(res==1) day1++;
                else day1+=2;
            }
            cout << day1 << '\n';
        }
    }
    return 0;
}

B

题目

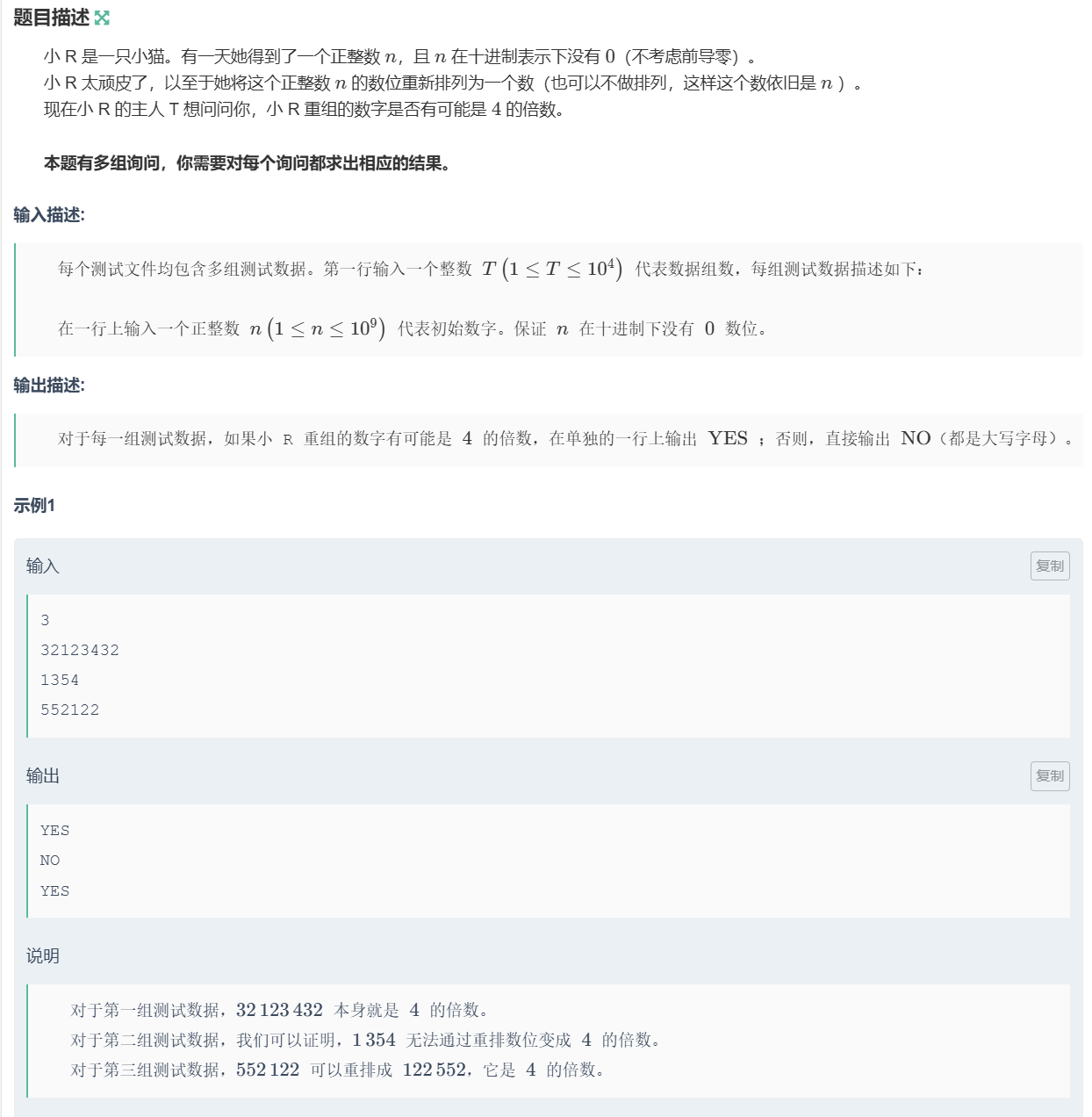
排列组合题，知道next_permutation()或者prev_permutation()以及stoi()会事半功倍

自己写字符串转数字容易tle，用stio()好些

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <bits/stdc++.h>
#define int long long
using namespace std;

signed main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t;
    cin >> t;
    while(t--){
        string cache;
        cin >> cache;
        sort(cache.begin(),cache.end());
        int pd=0;
        do{
            if((cache.back()-'0')%2) continue;
            int num = stoi(cache);
            pd = (num%4 ? 0:1); 
        }while(!pd && next_permutation(cache.begin(),cache.end()));
        cout << (pd==1 ? "YES\n":"NO\n");
    }
    return 0;
}

C

题目

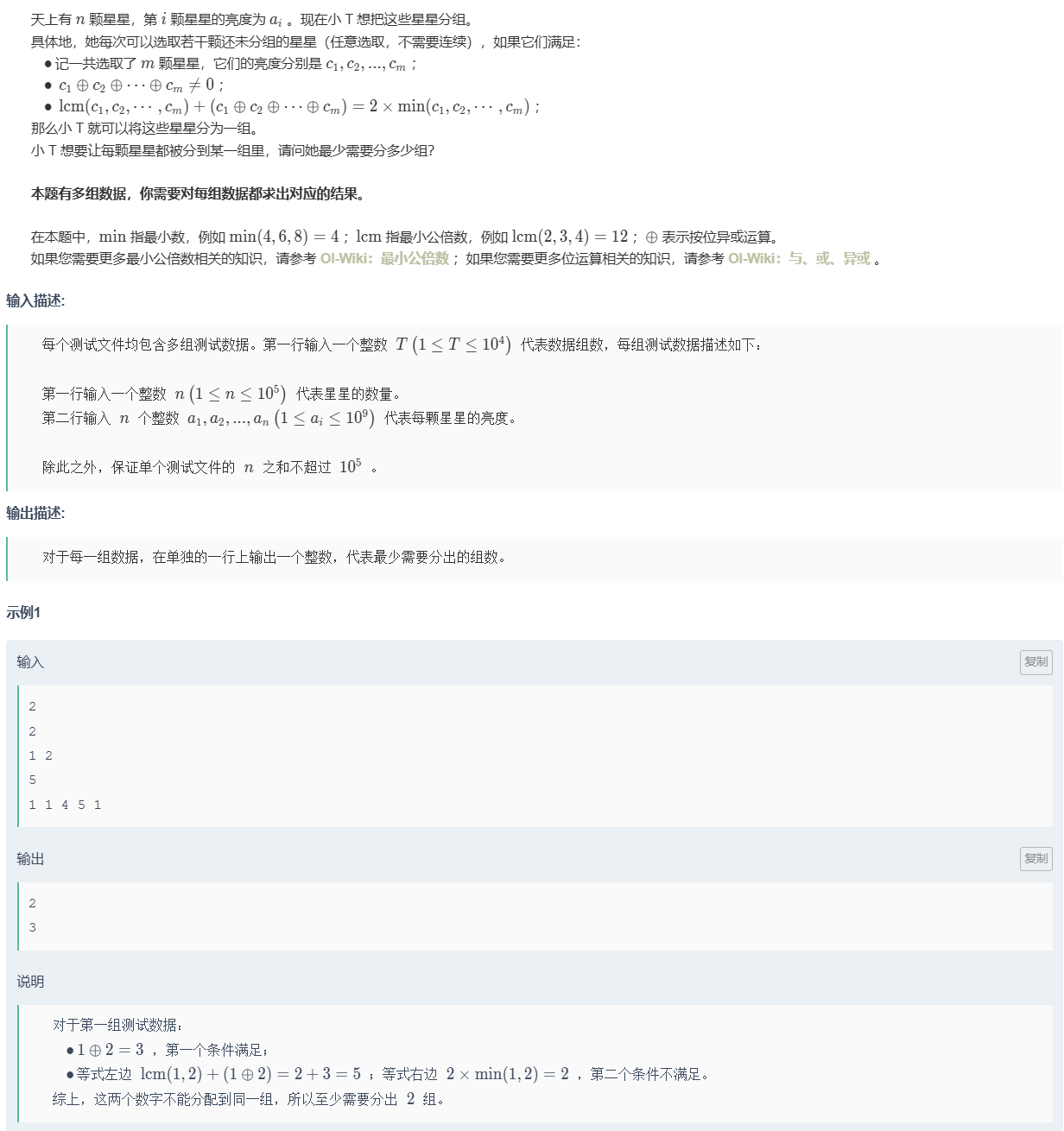
思维题，当时没开出来，看了发的题解思路后恍然大悟

第一个条件说明：异或不为0，那么一定大于零

第二个条件说明：lcm() + 一个大于零的数 =2*min()，

那么lcm() < 2*min() ①

由于lcm()一定是min()的倍数，倍数最小为2，即至少lcm() = 2*min() ②

由①和②得

所有数都相等，才能满足这俩条件

由于要异或不为0，因此某个数出现了奇数次则一定不为0，可一次删去

某个数出现了偶数次就要删两次

每个数删的次数之和 就是结果

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <bits/stdc++.h>
#define int long long
using namespace std;

signed main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t;
    cin >> t;
    while(t--){
        int n,cache,sum=0;
        map <int,int> m;
        set <int> s;
        cin >> n;
        for(int i=0;i<n;i++){
            cin >> cache;
            m[cache]++;
            s.insert(cache);
        }
        for(auto i:s){
            if(m[i]%2) sum++;
            else sum+=2;
        }
        cout << sum << '\n';
    }
    return 0;
}

D

题目

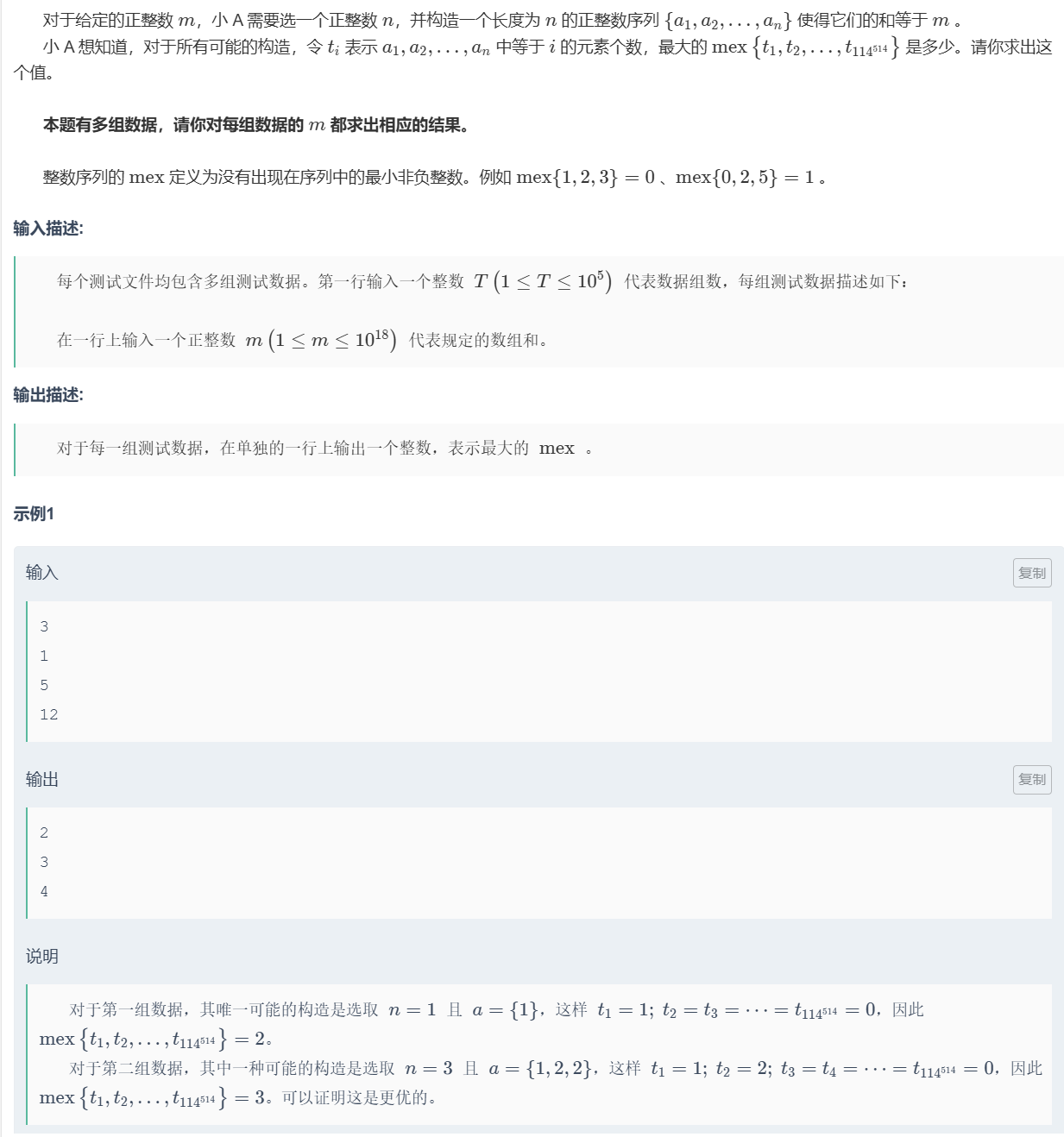
构造，根据贪心，要使得mex最大，那么越大的ti对应的i要越小，

即m >=(k^3+3k^2+2k)/6 ，输出k+1

可以用二分来找k

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>
#define int long long
#define check ((mid*mid*mid+3*mid*mid+2*mid) <= 6*m)
using namespace std;
const int maxn=2e6;

int binary(int m){
    int l=1,r=maxn,mid;
    while(l+1<=r){
        mid=(l+r+1)>>1;
        //cout<<"l:"<<l<<' ';
        //cout<<"r:"<<r<<' ';
        //cout<<"mid:"<<mid<<'\n';
        if((mid*mid*mid+3*mid*mid+2*mid) > 6*m){
            r=mid-1;
            //cout<<"new_r:"<<r<<'\n';
        }
        if((mid*mid*mid+3*mid*mid+2*mid) <= 6*m){
            l=mid;
            //cout<<"new_l:"<<l<<'\n';
        }
        cout << '\n';
    }
    return l;
}

signed main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t;
    cin >> t;
    while(t--){
        int m,k,l,r;
        cin >> m;
        k=binary(m);
        cout << k+1 << '\n';
    }
    return 0;
}

Algorithm学习

迭代加深搜索 IDDFS

当搜索树深度极深，宽度极广，DFS陷入递归无法返回、BFS队列空间直接爆炸，此时就可以采取迭代加深搜索 IDDFS

IDDFS结合了DFS和BFS。迭代过程上，在每一层的广度上采用了BFS，在具体实现上是DFS，大概的操作是：

  1. 先设定搜索深度为1,用DFS搜索到第1层即停止。也就是说，用DFS搜索一个

深度为1的搜索树。

  1. 如果没有找到答案，再设定深度为2,用 DFS 搜索前两层即停止。也就是说，用

DFS搜索一个深度为2的搜索树。

  1. 继续设定深度为3、4……逐步扩大 DFS的搜索深度，直到找到答案。

埃及分数可用IDDFS来解决

题目

该题的搜索树深度和宽度都可能是无穷的，所以要用IDDFS

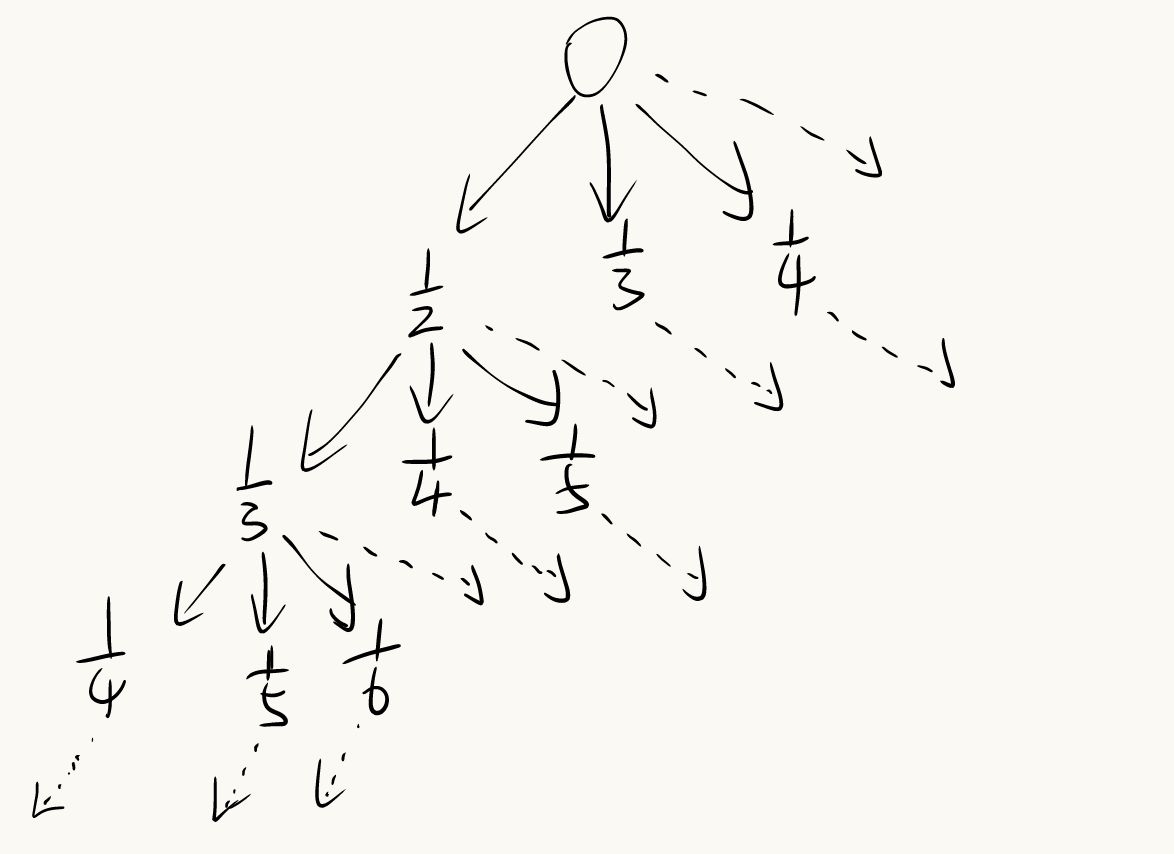
这一层找到了就不会去下一层找了，所以ans和temp的分母数量是相同的,也就是该层的层数

每一层搜索分母的起始值为i=b/a+1，i是分母，+1是因为找的分数要比题目给的分数小

每一层搜索分母的时候也有个限度，不可能无限搜吧，这个限度就是：

如果 剩余分母个数/分母 < 题目给的分数 ，即(deep-d+1)/i < a/b，那么这层就不用搜了，因为这层剩下的分数之和的最大值就是(deep-d+1)/i，如果这小于a/b了，那么这层分数再怎么累加也比a/b小。可以放缩证明，证明如下：

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 1e7;
int ans[maxn+2],temp[maxn+2],pd=0,deep;

int gcd(int a,int b){                    //欧几里得 
    return (b==0 ? a:gcd(b,a%b));
}

void simp(int &a,int &b){                //分数化简 
    int gys=gcd(a,b);
    a=a/gys;
    b=b/gys;
}

void iddfs(int a,int b,int d){
    //cout << "abc" << endl;
    if(d==deep){
        if(b%a) return;					//分子不为1，剪掉 
        if(temp[deep-1]==b/a) return; 	//分母重复，剪掉 
        pd=1;							//表示找到了 
        temp[d]=b/a;
        int pd1=0;
        if(ans[d]>temp[d]) memcpy(ans,temp,sizeof(int)*(d+1));
        return;
    }
    for(int i=max(temp[d-1]+1,b/a+1);;i++){	//i表示分母 
        if(b*(deep-d+1)<a*i) break;			//这不能用除法来判断，会陷入死循环(整除的原因); 
        temp[d]=i;
        // a/b-1/i=......
        //通分: (a*i-b)/b*i=......
        int a_1=a*i-b,b_1=b*i; 
        simp(a_1,b_1);
        iddfs(a_1,b_1,d+1);
    }
} 
signed main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int a,b;
    cin >> a >> b;
    simp(a,b);
    if(!b%a) cout << b/a << '\n';
    else{
        for(deep=2;;deep++){
            ans[1]=0,ans[deep]=maxn;	//初始化。要的是分母小的，所以最后一项先赋值最大，方便比较 
            iddfs(a,b,1);
            if(pd) break; 
        }
        for(int i=1;i<=deep;i++) cout << ans[i] << ' ';
        cout << '\n';
    }
    return 0;
}

最小公倍数

先求最大公约数gcd(a,b)

1
2
3
int gcd(int a,int b){
    return b==0 ? a : gcd(b,a%b);
}

,最小公倍数lcm(a,b)与其的关系为:

gcd(a,b)*lcm(a,b)=a*b

因此lcm(a,b)=(a*b)/gcd(a,b)

1
2
3
int lcm(int a,int b){
    return a/gcd(a,b)*b;
}

高精度

C++不像Java那样处理高精度非常简单，C++最大数据类型只有64位，如果要处理更大的数，只能用数组来模拟。

高精度算法本质上是用字符串模拟数字进行计算，再利用类似于数学里的竖式的形式，一位一位进行相关计算

读取数字，转为数组：

1
2
3
4
5
6
7
void read(int a[]) {
    string s;
    cin >> s; 
    len = s.size();
    for(int i=0;i<len;i++){
        a[i] = s[len-1-i] - '0';  //倒序存储
    }

进位、借位

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//加法进位: c[i] = a[i] + b[i]
 
if(c[i] >= 10) {
    c[i] -= 10;
    c[i+1]++;
}
 
//减法借位: c[i] = a[i] - b[i]
 
if(a[i] < b[i]) {
    a[i+1]--;
    a[i] += 10;   
} 
 
//乘法进位: c[i + j - 1] = a[i] * b[j] + x + c[i + j - 1];

x = c[i + j - 1] / 10;
c[i + j - 1] % 10;

高精度加法

从最低位开始，两加数相加，如果大于等于10，则高位++，该位-10

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void clear(int a[]){
  for(int i=0;i<len;i++) a[i] = 0;
}

void add(int a[], int b[], int c[]){
  clear(c);
  for(int i=0;i<len;i++){
    c[i] += a[i] +b [i];
    if(c[i] >= 10) {
        c[i] -= 10;
        c[i+1]++;
    }
  }
}

高精度减法

从最低位开始，两加数相减，如果小于0，则高位–，该位+10

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void clear(int a[]){
  for(int i=0;i<len;i++) a[i] = 0;
}

void sub(int a[], int b[], int c[]){
  clear(c);
  for(int i=0;i<len;i++){
    c[i] += a[i] - b[i];
    if(c[i] < 0){
        c[i] += 10;
        c[i+1] --;
    }
  }
}

这里需要注意，sub(a,b,c)只能处理a>b的情况，如果b>a的话需要另判，以下是完整的高精度减法代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <bits/stdc++.h>
using namespace std;
int a1,b1,pd=0,pd1=0;            //pd用于记录a1和b1，pd1用于判定a<b

void read(int a[]){
    string s;
    cin >> s;
    if(pd) a1=stoi(s),pd=1;
    else b1=stoi(s);
    int len=s.size();
    for(int i=0;i<len;i++)
        a[i] = s[len-1-i] -'0';
}

void sub(int a[],int b[],int c[]){
    for(int i=0;i<3;i++){
        c[i] += a[i]-b[i];
        if(c[i]<0){
            c[i+1]--;
            c[i]+=10;
        }
    }
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int a[3]={0},b[3]={0},c[3]={0};
    read(a);read(b);
    if(a1>b1) sub(a,b,c);			//a<b的判定
    else{
        sub(b,a,c);pd1=1;
    }
    if(pd1) cout << '-';
    for(int i=2;i>=0;i--){
        if(!c[i] && i!=0) continue;
        cout << c[i];
    }
    return 0;
}

高精度乘法

高精度 * 高精度 分解为 高精度 * 单精度，再进行计算。

这里直接计算结果中的从低到高第 i 位，且一并处理了进位，第 i 次循环为 c[i] 加上了所有满足 p + q = i 的 a[p] 与 b[q] 的乘积之和，更为简短

1
2
3
4
5
6
7
8
9
10
11
12
void mul(int a[], int b[], int c[]) {
  clear(c);

  for(int i=0;i<len;i++){        //b是i，a是j
    for(int j=0;j<=i;j++) 
        c[i]+= a[j] * b[i-j];
    if(c[i] >= 10){
      c[i+1] += c[i] / 10;
      c[i] %= 10;
    }
  }
}

高精度除法

高精度除法可以模拟竖式除法，看作一个逐次减法的过程

这里得到被除数的长度la与除数的长度lb，从下标la-lb开始，从高位到低位来计算商，减少了冗余运算。 被除数 a 以下标 last_dg 为最低位，是否可以再减去除数 b 而保持非负

，len 是除数 b 的长度，避免反复计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

bool greater_eq(int a[], int b[], int last_dg, int length){
  if(a[last_dg+length] != 0) return true;
  for(int i = length-1;i>=0;i--){
    if(a[last_dg+i] > b[i]) return true;
    if(a[last_dg+i] < b[i]) return false;
  }
  return true;
}

void div(int a[], int b[], int c[], int d[]){
  clear(c);
  clear(d);
  int la, lb;
  for(la=len-1;la>0;la--)
    if(a[la-1] != 0) break;
  for(lb=len-1;lb>0;lb--)
    if(b[lb-1] != 0) break;
  if(lb==0){  //除数不为零
    puts("NO");
    return;
  }

  // c 是商，d是被除数剩余部分
  for(int i=0;i<la;i++) d[i] = a[i];
  for(int i=la-lb;i>=0;i--){
    // 计算商的第 i 位，这里la-lb可以减少计算量
    while(greater_eq(d, b, i, lb)){
      for(int j=0;j<lb;j++){
        d[i+j] -= b[j];
        if(d[i+j] < 0){
          d[i+j+1] -= 1;
          d[i+j] += 10;
        }
      }
      c[i] += 1;
    }
  }
}

并查集

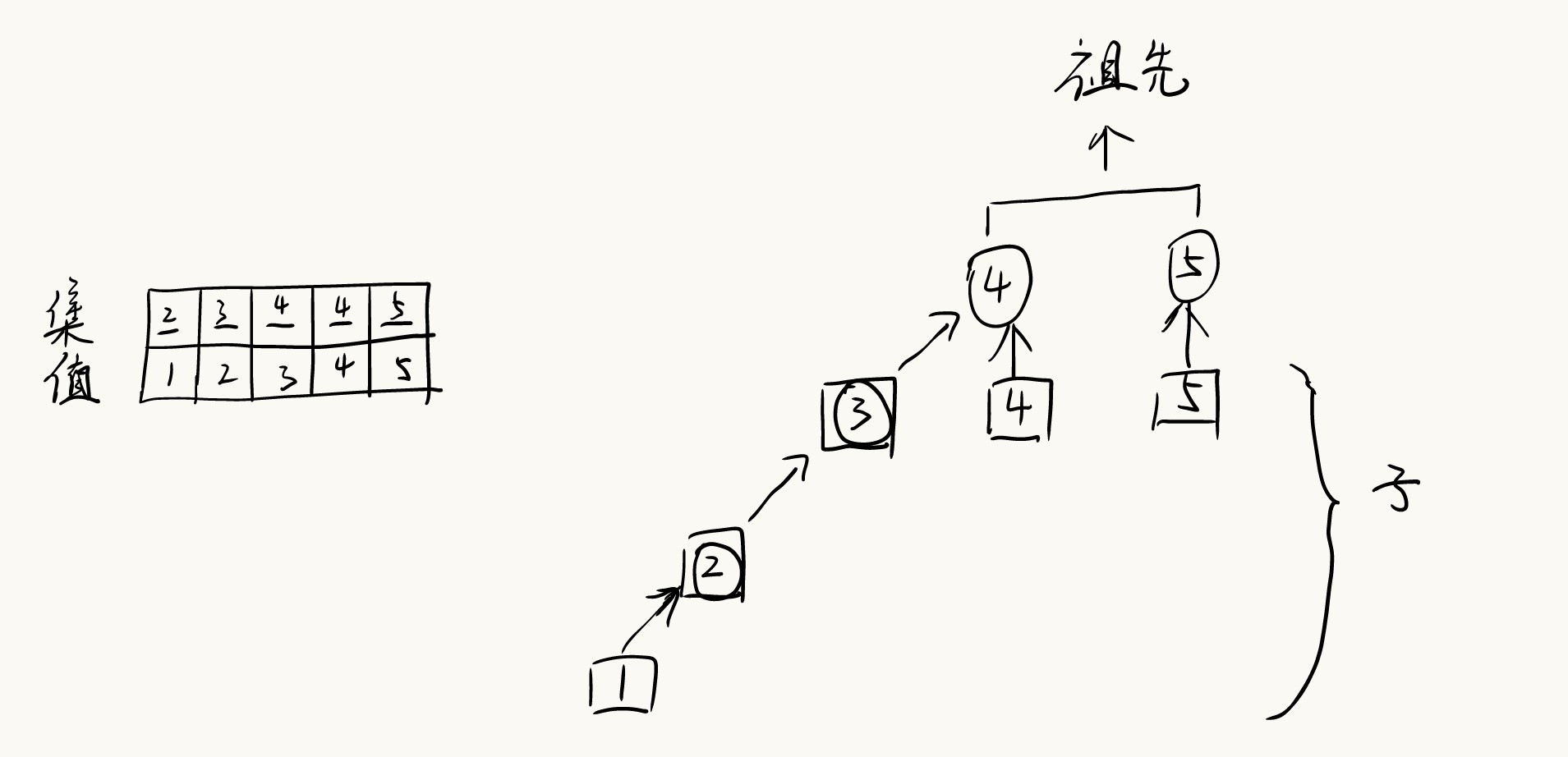
将编号分别为1~n的n个对象划分为不相交集合，在每个集合中，选择其中某个元素代表所在集合。在这个集合中，并查集的操作有初始化，合并，查找。

合并：合并两个元素所属集合（合并对应的树）

查询：查询某个元素所属集合（查询对应的树的根节点，也就是祖先），这可以用于判断两个元素是否属于同一集合

用并查集的基础操作完成HDU 1213

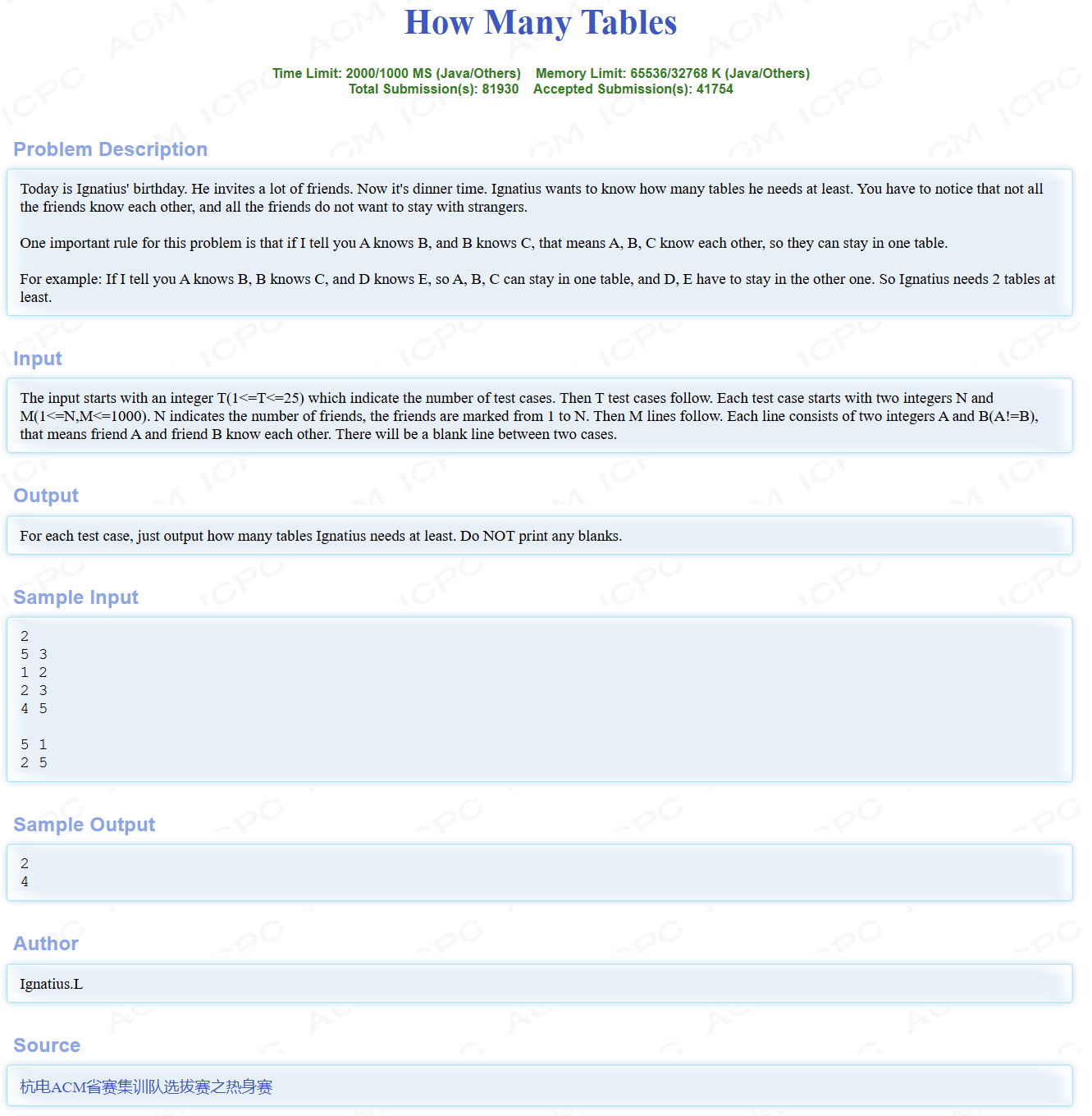
题目

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <bits/stdc++.h>
using namespace std;
int s[1005];

int find_s(int x){
    return (x==s[x] ? x:find_s(s[x]));
}

void union_s(int a,int b){
    int x=find_s(a),y=find_s(b);
    if(x!=y) s[x]=s[y];
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t;
    cin >> t;
    while(t--){
        int n,m,a,b,sum=0;
        cin >> n >> m;
        for(int i=0;i<1005;i++) s[i]=i;
        for(int i=1;i<=m;i++){
            cin >> a >> b;
            union_s(a,b);
        }
        for(int i=1;i<=n;i++)
            if(s[i]==i) sum++;
        cout << sum << '\n';
    }
    return 0;
}

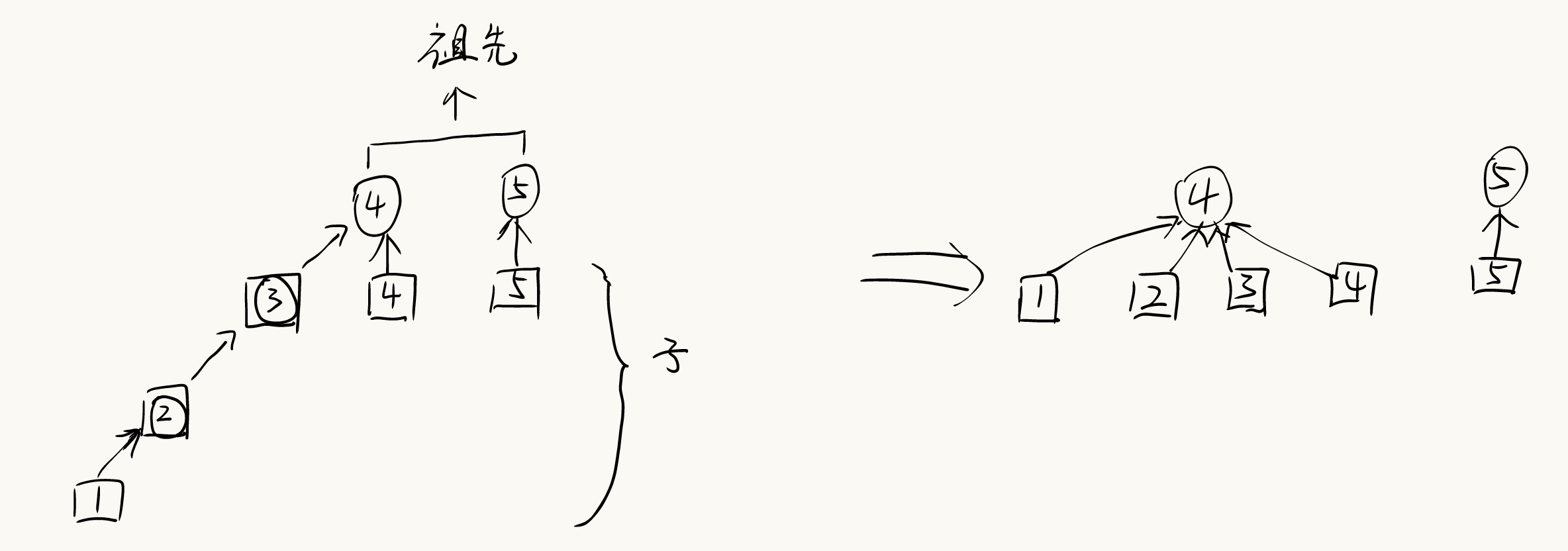
路径压缩

在合并过程中，树可能会发生退化，退成链表，增加查询的时间复杂度。通过路径压缩，将所有的子节点直接连到根节点，可大幅缩短搜索路径，加快查询

1
2
3
int find_s(int x){
    return (x==s[x] ? x : s[x]=find_s(s[x]));
}