2024下 第14周12.2~12.8

codeforces 22 div2(喔被豹纱了)

A

题目

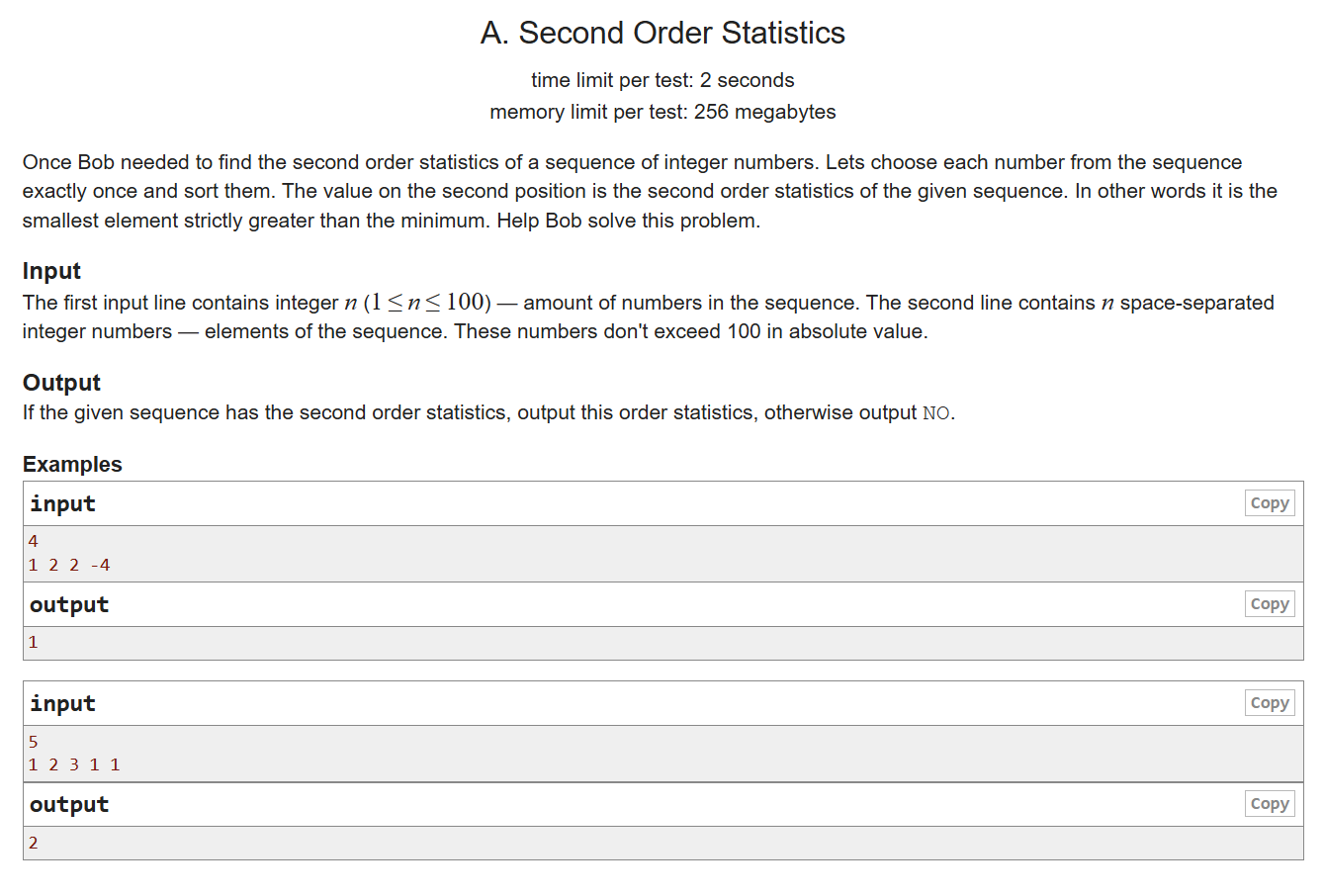
签到题，利用set的互异性和自动排序就可以

代码

#include <bits/stdc++.h>
using namespace std;

int n,ip;
set <int> s;
int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n;
    for(int i=0;i<n;i++){
        cin >> ip;
        s.insert(ip);
    }
    set<int>::iterator it;
    it = s.begin();it++;
    if(it!=s.end()) cout << *it;
    else cout << "NO";
    return 0;
}

B

题目

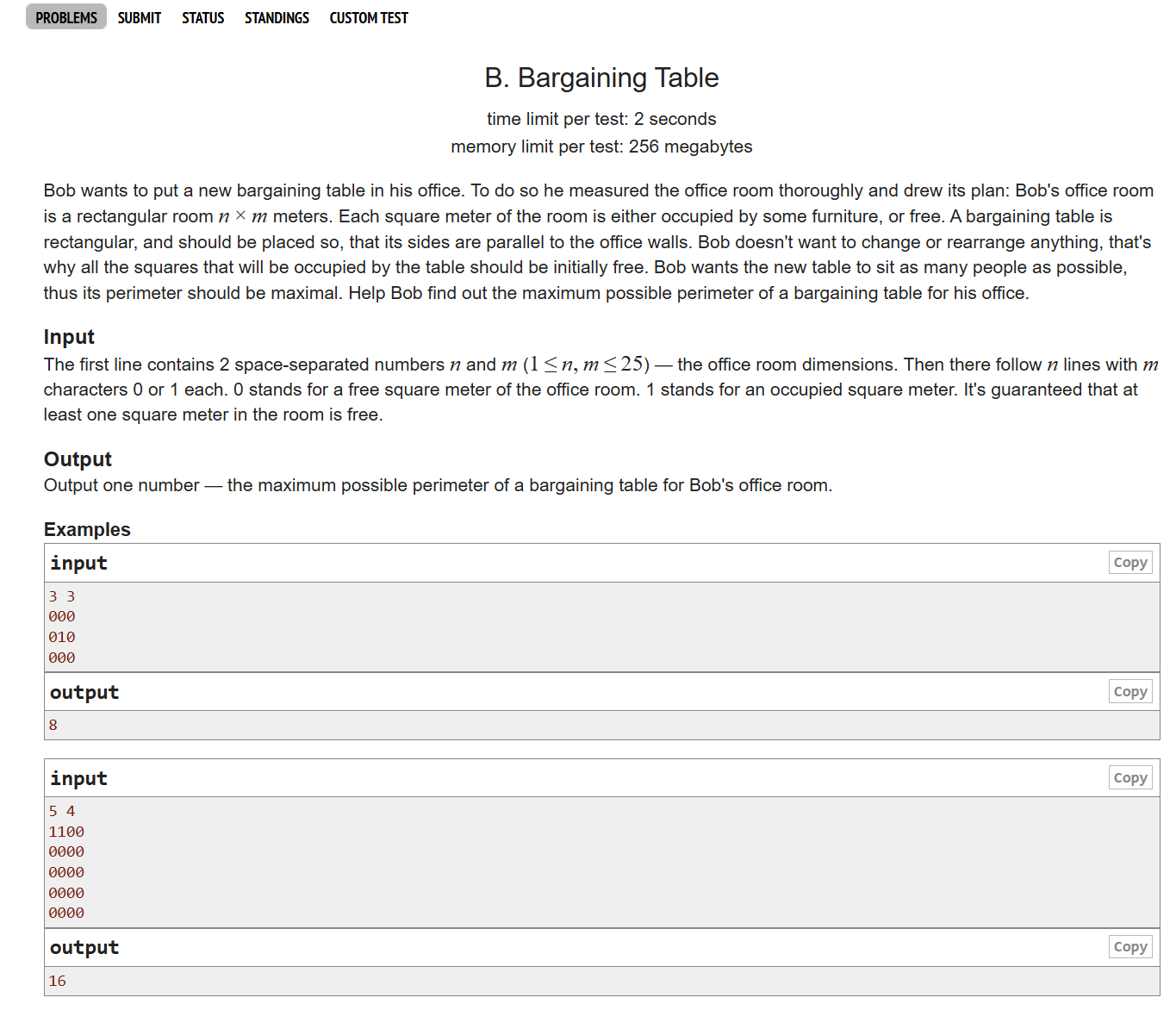
这道题取值范围很小，暴力速解。就是判断一个矩阵里是否含"1"，是就pass，否就更行周长c

代码

#include <bits/stdc++.h>
using namespace std;

int n,m,c=0;
char room[26][26];
bool check(int x1,int y1,int x2,int y2){
    for(int i=x1;i<=x2;i++)
        for(int j=y1;j<=y2;j++)
            if(room[i][j]=='1') return 0;
    return 1;
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n >> m;
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
            cin>>room[i][j];
    for(int x_1=0;x_1<n;x_1++)
        for(int y_1=0;y_1<m;y_1++)
            for(int x_2=x_1;x_2<n;x_2++)
                for(int y_2=y_1;y_2<m;y_2++)
                    if(check(x_1,y_1,x_2,y_2)) c=max(c,(x_2-x_1+1+y_2-y_1+1)*2);
    cout << c;
    return 0;
}

C

题目

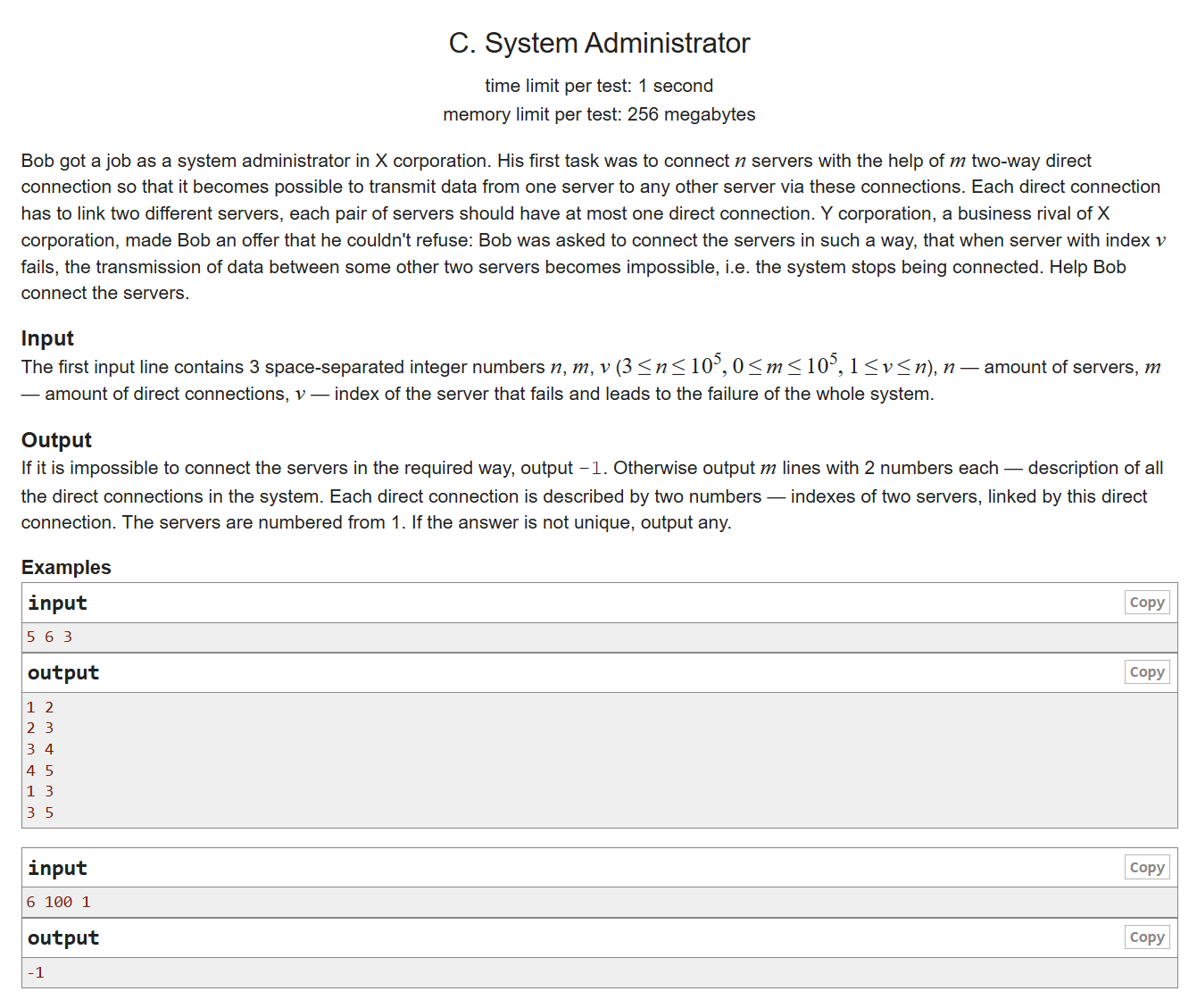
一道图论题，此题将我引进了图论的大门。根据情况排除一个顶点(要么排除第一个，要么排除最后一个)后，剩下的顶点往完全图上凑。需要注意的是特殊情况的公式(n-1)*(n-2))/2+1

(WC这题是真的很难读懂啊，用翻译插件翻译成中文也不知道出题人在BB啥)

代码

#include <bits/stdc++.h>
using namespace std;

int n,m,v,End,start,pai;

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n >> m >> v;
    if(m > ((n-1)*(n-2))/2+1 || m < n-1) cout << -1;
    else{
        if(v==n){
            start=2;End=n;pai=1;
        }
        else{
            start=1;End=n-1;pai=n;
        }
        cout << v <<' '<< pai<<'\n';
        for(int i=start;i<End;i++){
            if(m==1) break;
            for(int j=i+1;j<=End;j++){
                if(m==1) break;
                cout << i <<' '<< j << '\n';
                m--;
            }
        }
    }	
    return 0;
}

D

题目

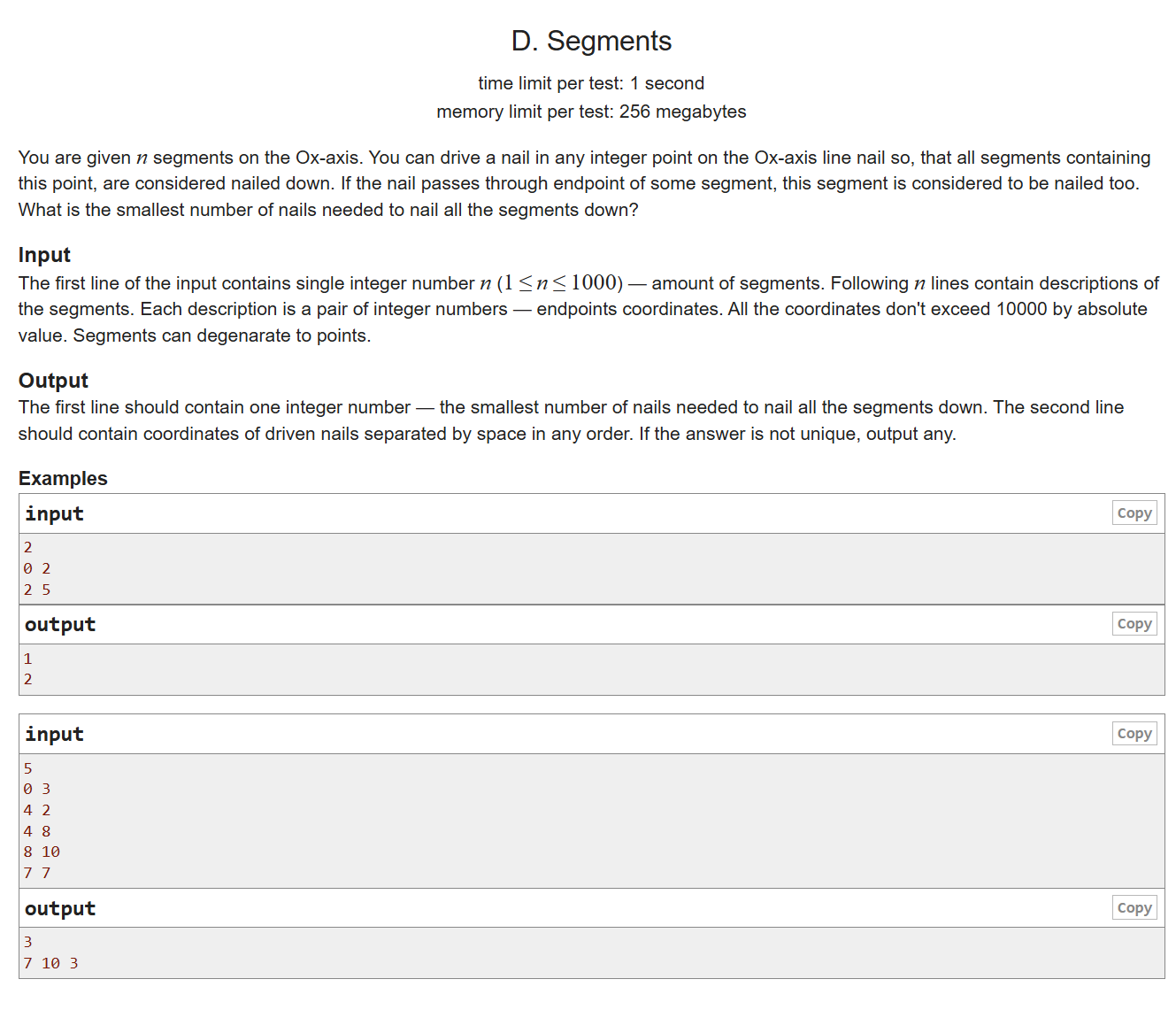
这是一道贪心题。先对每个区间的右端点进行排序，然后取右端点的值，如果该值在下n个区间内，那么下n个区间都是被这个"钉子"钉住的。如果不在下个区间内，则下个区间未被钉住，那么更行该值——取下个区间的右端点。

代码

#include <bits/stdc++.h>
using namespace std;

int n,x1,x2,nail=10001;
vector <int> ans;
struct seg{
    int l; int r;
}qu[1001];
bool cpa(seg x,seg y){
    return x.r < y.r;
}
int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n;
    for(int i=0;i<n;i++){
        cin >> x1 >> x2;
        if(x1 > x2) swap(x1,x2);
        qu[i].l=x1;qu[i].r=x2;
    }
    sort(qu,qu+n,cpa);
    for(int i=0;i<n;i++){
        if(nail >= qu[i].l && nail <= qu[i].r) continue;
        nail = qu[i].r;
        ans.push_back(nail);
    }
    cout << ans.size() << '\n';
    for(auto i:ans) cout << i << ' ';
    return 0;
}

codeforces 640 div4

A

题目

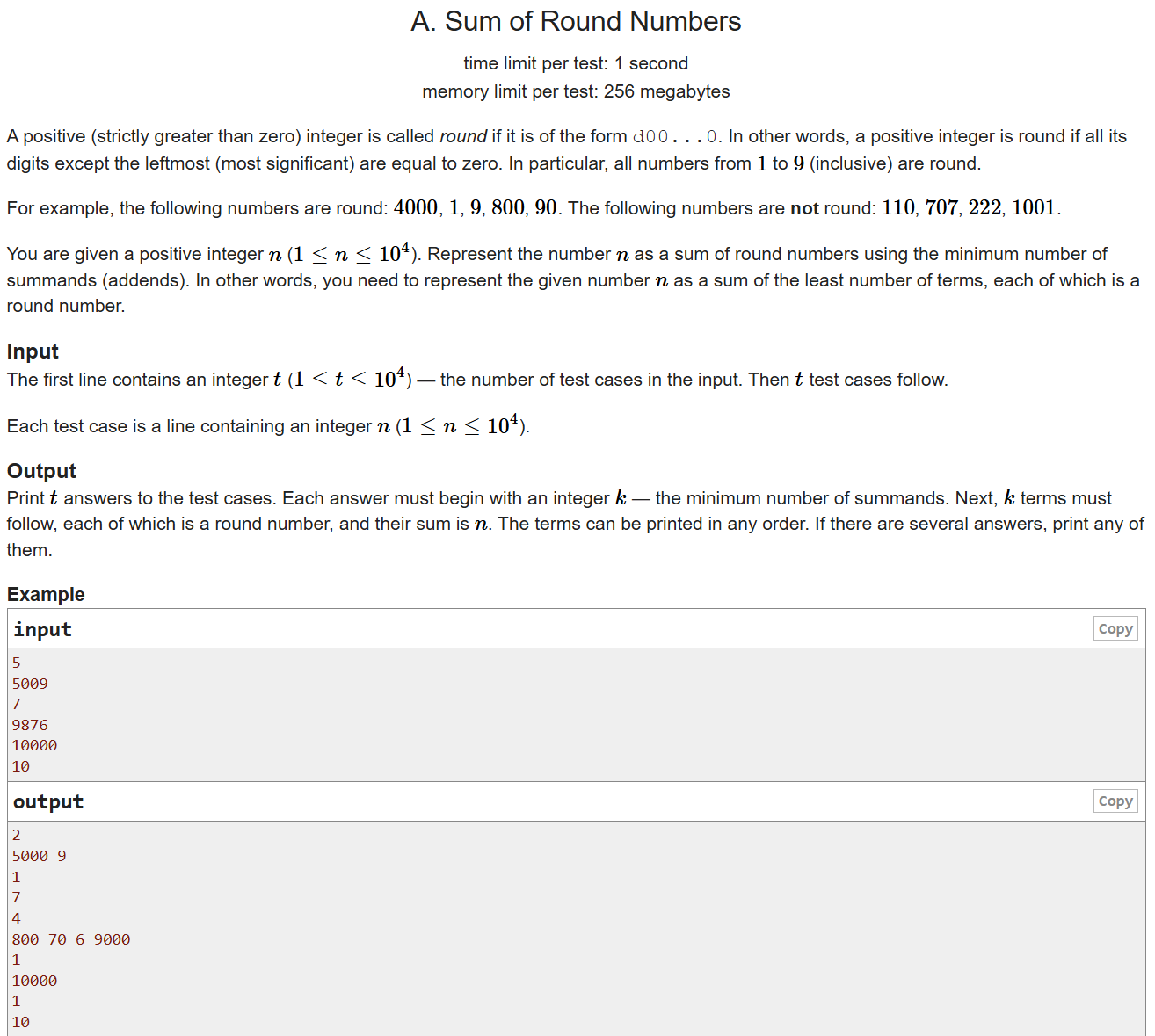
签到数学题，就是对多位数进行拆分，例如5108拆成5000，100，8

代码

#include <bits/stdc++.h>
using namespace std;

int t,sum,n,a,wei=1;
vector <int> num;
int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> t;
    for(int i=0;i<t;i++){
        cin >> n;
        wei=1;
        while(n){
            a = n%10;
            if(a!=0) num.push_back(a*wei);
            wei *= 10;
            n /=10;
        }
        cout << num.size() << '\n';
        for(auto i:num) cout << i <<' ';
        cout << '\n';
        num.clear();
    }	
    return 0;
}

B

题目

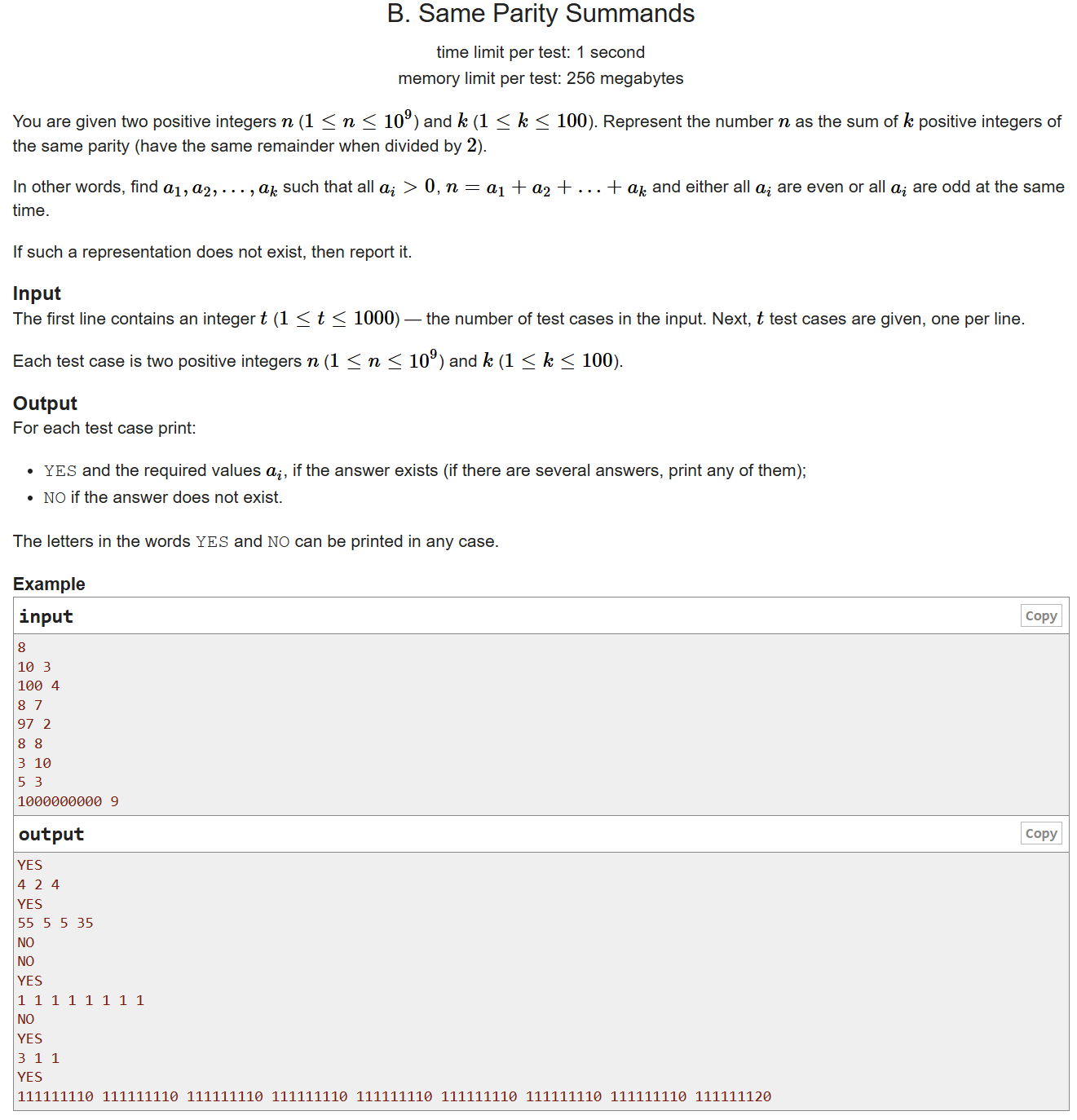
数学题，此题有技巧，找特殊情况。如果a > b并且a-(b-1)是奇数，那么可以凑成特殊情况——b-1个1加上a-(b-1)1；如果a>2b并且a-(b-1)*2是偶数，那么可以凑成特殊情况——b-1个2加上a-(b-1)*2

代码

#include <bits/stdc++.h>
using namespace std;

int n,a,b;

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n;
    for(int i=0;i<n;i++){
        cin >> a >> b;
        if(a>=b && (a-b+1)%2==1){
            cout << "YES" << '\n';
            for(int j=0;j<b-1;j++) cout << 1 << ' ';
            cout << a-b+1 << '\n';
        }
        else if(a>=2*b && (a-(b-1)*2)%2==0){
            cout << "YES" << '\n';
            for(int j=0;j<b-1;j++) cout << 2 << ' ';
            cout << a-(b-1)*2 << '\n';
        }
        else cout << "NO" << '\n';
    }	
    return 0;
}

C

题目

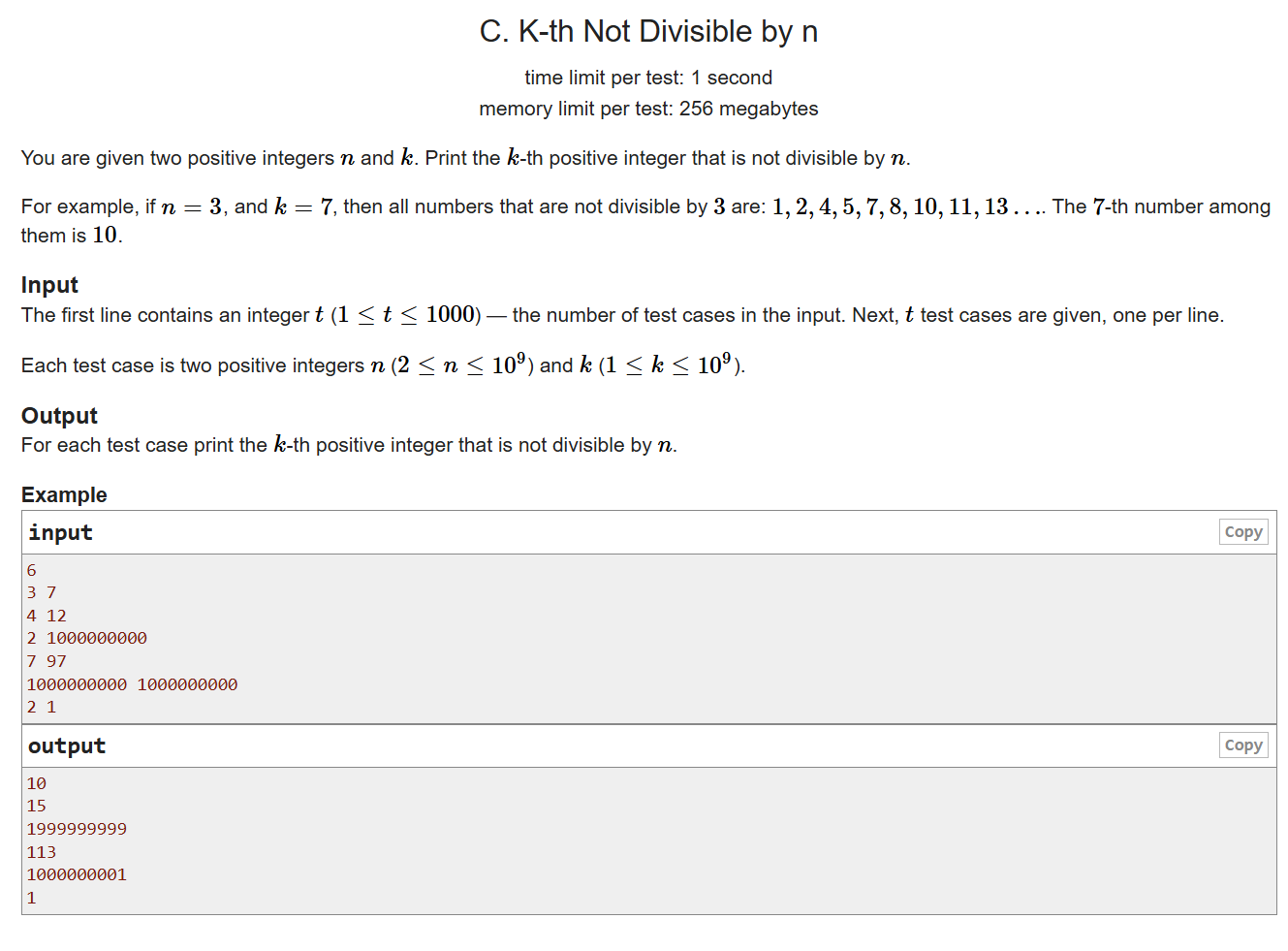
我了个豆啊又是数学题，数学题就要找寄巧。

将所有正整数从1到+∞ 每n个数分一组，那么每个小组里有n-1个数不能被n整除

这就是关键。注意一下特殊情况(k恰好能整除n-1)就行

代码

#include <bits/stdc++.h>
using namespace std;
int t,n,k,a1,a2;
int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> t;
    for(int i=0;i<t;i++){
        cin >> n >> k;
        a1= k/(n-1);
        a2= k%(n-1);
        if(a2 == 0) cout << a1*n+a2-1 << '\n';
        else cout << a1*n+a2 << '\n';
    }
    return 0;
}

D

题目

这题干更是逆天玩意，一看一个不吱声，典型烦人模拟题。

模拟题也不用什么算法，这里注意goto的语句的位置

代码

#include <bits/stdc++.h>
using namespace std;

int t,n,a,sumr=0,suml=0,r=0,l=0,ci=1,zhi=0;
deque <int> arr;
int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> t;
    for(int i=0;i<t;i++){
        cin >> n;
        for(int j=0;j<n;j++){
            cin >> a;
            arr.push_back(a);
        }
        r += arr.front();
        sumr +=r;
        arr.pop_front();
        while(1){
            if(arr.empty()) break;
            l=0;zhi=0;
            while(l <= r){
                if(arr.empty() && zhi==0){
                    suml+=l;goto en2;
                }else if(arr.empty()){
                    suml+=l;goto en1;
                }
                l += arr.back();
                arr.pop_back();
                zhi++;
            }
            suml+=l;
            ci++;
            r=0;zhi=0;
            while(r <= l){
                if(arr.empty() && zhi==0){
                    sumr+=r;goto en2;
                }else if(arr.empty()){
                    sumr+=r;goto en1;
                }
                r += arr.front();
                arr.pop_front();
                zhi++;
            }
            sumr+=r;
            ci++;
        }
        en2:cout << '\n' << ci<<' '<<sumr<<' '<<suml<<'\n';
        arr.clear();sumr=0;suml=0;r=0;l=0;ci=1;
        continue;
        en1:ci++;
        cout << '\n' << ci<<' '<<sumr<<' '<<suml<<'\n';
        arr.clear();sumr=0;suml=0;r=0;l=0;ci=1;
    }
    return 0;
}

算法训练

BFS

马的遍历–洛谷P1143

为减少屏占，题目以图片形式放出

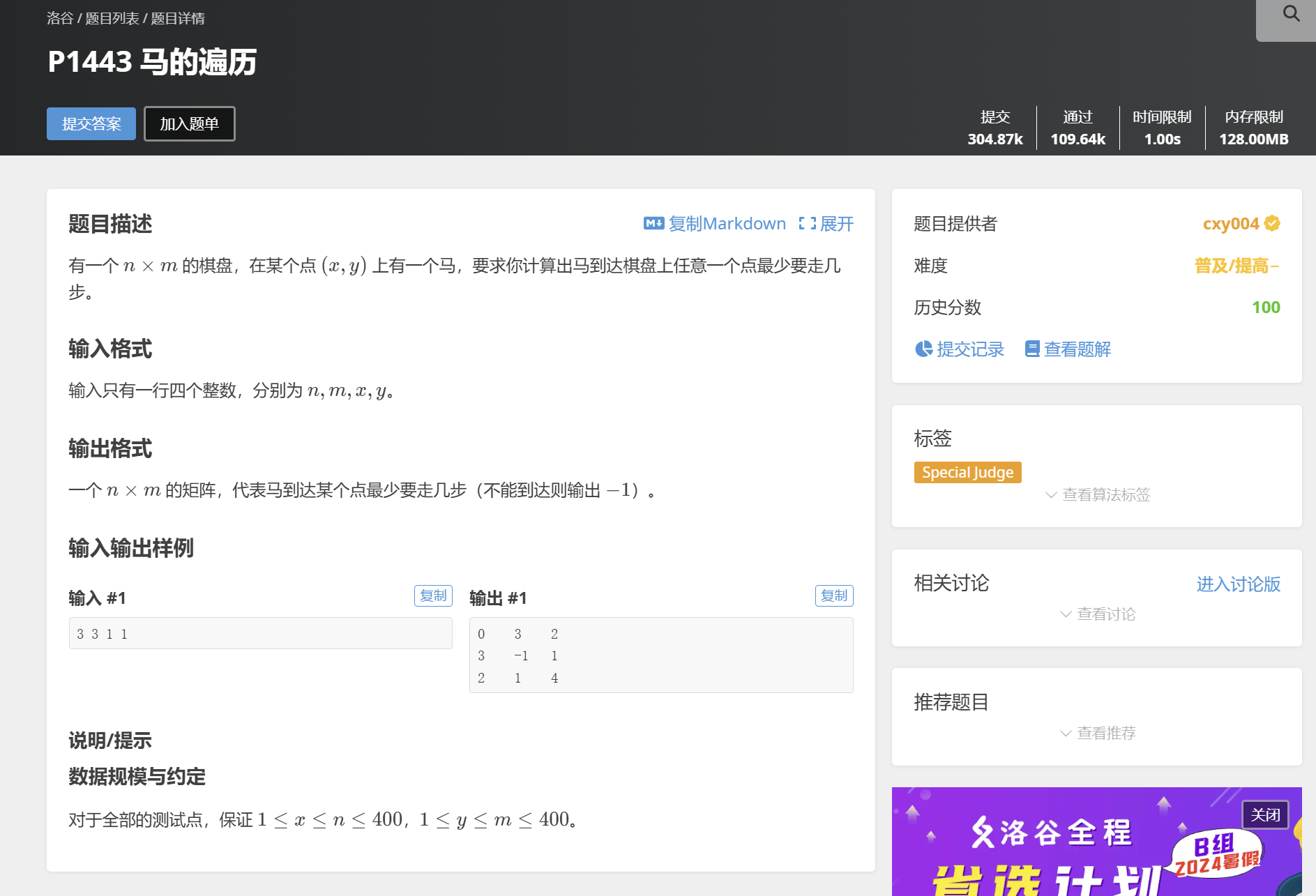
一道经典的BFS搜索题目。

马的前进用BFS+queue解决；到每个可到达点的最少步数，选择用dp递推来累计

#include <bits/stdc++.h>
using namespace std;

int n,m,x,y,room[401][401],steps[401][401];
int explore[][2]={1,2,2,1,-1,-2,-2,-1,1,-2,2,-1,-1,2,-2,1};
struct horse{int x;int y;};
#define check(x,y) (x>=0 && x<n && y>=0 && y<m)
void BFS(int sx,int sy){
    queue <horse> q;
    horse start,next;
    start.x=sx; start.y=sy;
    q.push(start);
    while(!q.empty()){
        start=q.front();
        q.pop();
        for(int i=0;i<8;i++){
            next.x = start.x + explore[i][0];
            next.y = start.y + explore[i][1];
            if(check(next.x,next.y) && room[next.x][next.y]==0){
                room[next.x][next.y]=1;
                steps[next.x][next.y]=steps[start.x][start.y]+1;
                q.push(next);
            }
        }
        
    }
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n >> m >> x >> y;
    x--; y--;
    fill_n(&steps[0][0],401*401,-1);
    room[x][y]=1;
    steps[x][y]=0;
    BFS(x,y);
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            cout << steps[i][j] << ' '; 
        }
        cout << '\n';
    }
    return 0;
}

DP

硬币问题

1.最小硬币问题

题目描述：

有n种硬币，面值分别为v1,v2,…,vn，数量无限。输入非负整数s，选用硬币，使其和为s。要求输出最少的硬币组合。

这是一道DP题目，minnum[j]表示要凑到 j 元所需最小的硬币数量。

状态转移方程为minnum[j]=min(minnum[j],minnum[j-money[i]]+1)

代码

#include <bits/stdc++.h>
using namespace std;

int value,minnum[251],money[5]={1,5,10,20,50};

void mincoin(int *value){
    for(int i=0;i<5;i++)
        for(int j=money[i];j<=*value;j++)
            minnum[j]=min(minnum[j],minnum[j-money[i]]+1);
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    fill_n(&minnum[0],251,INT_MAX);
    minnum[0]=0;
    cin >> value;
    mincoin(&value);
    cout << minnum[value] <<'\n';
    return 0;
}

硬币问题未完待续…